2023-2024学年初中数学八年级上册 13.3 全等三角形的判定 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 如图,已知 , 如果只添加一个条件(不加辅助线)使ΔABC≌ΔDEC,则添加的条件不能为( )
 A、 B、 C、 D、2. 如图,已知是的中线,E、F分别是和延长线上的点,且 , 连接 , 下列说法中:①;②;③;④ . 正确的是( )
A、 B、 C、 D、2. 如图,已知是的中线,E、F分别是和延长线上的点,且 , 连接 , 下列说法中:①;②;③;④ . 正确的是( )
 A、①②③ B、①②④ C、①③④ D、②③④3. 如图,已知 , 如果只添加一个条件(不加辅助线)使 , 则添加的条件不能为( )
A、①②③ B、①②④ C、①③④ D、②③④3. 如图,已知 , 如果只添加一个条件(不加辅助线)使 , 则添加的条件不能为( ) A、 B、 C、 D、4. 如图,在和中, , , 添加一个条件后,你无法判定的是( )
A、 B、 C、 D、4. 如图,在和中, , , 添加一个条件后,你无法判定的是( ) A、 B、 C、 D、5. 如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是 , 当小敏从水平位置下降时,小明离地面的高度是( )
A、 B、 C、 D、5. 如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是 , 当小敏从水平位置下降时,小明离地面的高度是( )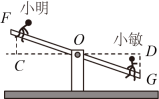 A、 B、 C、 D、6. 如图,在和中, , 是的中点, , 垂足为点 , 且 . 若 , 则的长为( )
A、 B、 C、 D、6. 如图,在和中, , 是的中点, , 垂足为点 , 且 . 若 , 则的长为( ) A、2cm B、 C、 D、7. 乐乐所在的七年级某班学生到野外活动,为测量池塘两端 , 的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:
A、2cm B、 C、 D、7. 乐乐所在的七年级某班学生到野外活动,为测量池塘两端 , 的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:乐乐:如图 , 先在平地取一个可直接到达 , 的点 , 再连接 , , 并分别延长至 , 至 , 使 , , 最后测出的长即为 , 的距离.
明明:如图 , 先过点作的垂线 , 再在上取 , 两点,使 , 接着过点作的垂线 , 交的延长线于点 , 则测出的长即为 , 的距离.
聪聪:如图 , 过点作 , 再由点观测,在的延长线上取一点 , 使这时只要测出的长即为 , 的距离.
以上三位同学所设计的方案中可行的是( )
 A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行8. 如图,在五边形ABCDE中, , , 则五边形ABCDE的面积等于( )
A、乐乐和明明 B、乐乐和聪聪 C、明明和聪聪 D、三人的方案都可行8. 如图,在五边形ABCDE中, , , 则五边形ABCDE的面积等于( )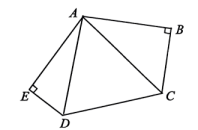 A、16 B、20 C、24 D、26
A、16 B、20 C、24 D、26二、填空题
-
9. 如图,A,两点分别位于一个池塘的两端,小凡想用绳子测量A,间的距离,但无法从A点直接到达点,聪明的小凡想出一个办法:先在地上选取一个可以直接到达点的点 , 连接 , 取的中点(点可以直接到达A点),连接并延长到点 , 使 . 连接 , 并测量出它的长度为10米,则A,两点间的距离为米.
 10. 如图,已知B,D,C,F在同一条直线上, , , , 若 , , 则 .
10. 如图,已知B,D,C,F在同一条直线上, , , , 若 , , 则 . 11. 如图,已知D是△ABC的边BC上一点,且 , , AE是△ABD的中线,若 , 则 .
11. 如图,已知D是△ABC的边BC上一点,且 , , AE是△ABD的中线,若 , 则 . 12. 已知正方形的边长为 , 点E是边上一点, , 连接 , 将绕点D旋转 , 得到 , 则的面积为 .13. 如图8,正方形ABCD的边长为8,对角线AC,BD相交于点O,点M,N分别在边BC,CD上,且∠MON=90°,连接MN交OC于P,若BM=2,则OP·OC=.
12. 已知正方形的边长为 , 点E是边上一点, , 连接 , 将绕点D旋转 , 得到 , 则的面积为 .13. 如图8,正方形ABCD的边长为8,对角线AC,BD相交于点O,点M,N分别在边BC,CD上,且∠MON=90°,连接MN交OC于P,若BM=2,则OP·OC=.
三、解答题
-
14. 如图,在中, , 垂足为点 , 点在上,为的中点,连接并延长至点 , 使得 , 连接 . 请判断线段与线段的关系,并说明理由.

四、综合题
-
15. 小琳在学习等腰三角形性质“三线合一”时,发现:
 (1)、如图1,在中,若 , 可以得出 . 请你用所学知识证明此结论.(2)、小琳提出了一个问题:如图2,如果 , 能不能说明?小琳不知道这个问题如何解决,便询问老师,老师进行了指导:条件里有“”和“”,我们可以尝试将和 “变成”一条线段,将和 “变成”一条线段,为了确保的条件可以使用,和的位置最好不要改变,所以我们可以“延长至E,使 , 延长至F,使”.老师指导后,小琳还是没有思路.请你帮助小琳,完成问题的解答,(3)、小琳又提出了新的问题:如图3,如果 , 能不能说明?请你帮助小琳,完成问题的解答.16.
(1)、如图1,在中,若 , 可以得出 . 请你用所学知识证明此结论.(2)、小琳提出了一个问题:如图2,如果 , 能不能说明?小琳不知道这个问题如何解决,便询问老师,老师进行了指导:条件里有“”和“”,我们可以尝试将和 “变成”一条线段,将和 “变成”一条线段,为了确保的条件可以使用,和的位置最好不要改变,所以我们可以“延长至E,使 , 延长至F,使”.老师指导后,小琳还是没有思路.请你帮助小琳,完成问题的解答,(3)、小琳又提出了新的问题:如图3,如果 , 能不能说明?请你帮助小琳,完成问题的解答.16. (1)、【操作发现】如图1是一个长为、宽为的长方形,沿图1中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).那么图2中的阴影部分的面积为:(用a,b的代数式表示);观察图2,请你写出 , , 之间的等量失系是;(2)、【灵活应用】运用所得到的公式计算:若x,y为实数,且 , , 求的值;(3)、【拓展迁移】将两块全等的特制直角三角板 , 按如图3所示的方式放置,A,O,D在同一直线上,连接AC,BD.若 , , 求阴影部分的面积.17. 在中, , , 点D是AC边上一点,交于点F,交直线于点E.
(1)、【操作发现】如图1是一个长为、宽为的长方形,沿图1中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).那么图2中的阴影部分的面积为:(用a,b的代数式表示);观察图2,请你写出 , , 之间的等量失系是;(2)、【灵活应用】运用所得到的公式计算:若x,y为实数,且 , , 求的值;(3)、【拓展迁移】将两块全等的特制直角三角板 , 按如图3所示的方式放置,A,O,D在同一直线上,连接AC,BD.若 , , 求阴影部分的面积.17. 在中, , , 点D是AC边上一点,交于点F,交直线于点E. (1)、如图1,当D为的中点时,证明: .(2)、如图2,若于点M,当点D运动到某一位置时恰有 , 则与有何数量关系,并说明理由.(3)、连接 , 当时,求的值.
(1)、如图1,当D为的中点时,证明: .(2)、如图2,若于点M,当点D运动到某一位置时恰有 , 则与有何数量关系,并说明理由.(3)、连接 , 当时,求的值.
-