2023-2024学年初中数学八年级上册 13.2 全等图形同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $△ A B C ≌ △ D E C$ ，点B，C，D在同一条直线上，且 $C E = 1$ ， $C D = 3$ ，则 $B D$ 的长是（）

A、 $1.5$ B、2 C、4 D、6

查看试题解析
2. 如图， $△ A B C ≌ △ D E F$ ，若 $A C = 5$ ， $C F = 2$ ，则 $C D$ 的长为（）

A、2 B、2.5 C、3 D、5

查看试题解析
3. 如图，在 $3 \times 3$ 的正方形网格中， $∠ 1 + ∠ 2$ 等于（）

A、60° B、75° C、90° D、105°

查看试题解析
4. 如图1，在 $Δ A B C$ 中， $∠ B = 80 °$ ， $∠ C = 30 °$ ．若 $△ A B C ≌ △ A D E$ ， $∠ D A C = 32 °$ ，则 $∠ E A C$ 的度数为（）

A、18° B、30° C、32° D、38°

查看试题解析
5. 如图， $△ A B C ≌ △ A D E$ ，点D在BC上，下列结论中不一定成立的是（）

A、 $∠ E = ∠ C$ B、 $B C = D E$ C、 $∠ B A D = ∠ C A E$ D、 $A B = B D$

查看试题解析
6. 如图，已知在正方形 $A B C D$ 中， $A B = B C = C D = A D = 10$ 厘米， $∠ A = ∠ B = ∠ C = ∠ D = 9 0^{°}$ ，点E在边 $A B$ 上，且 $A E = 4$ 厘米，如果点P在线段BC上以2厘米／秒的速度由B点向C点运动，同时，点Q在线段 $C D$ 上由C点向D点运动，设运动时间为t秒，当ΔBPE与ΔCQP全等时，t的值为（　　）

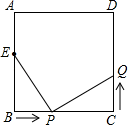A、2 B、2或1.5 C、2.5 D、2.5或2

查看试题解析
7. 如图，四边形 $A B C D$ 中， $A D / / B C$ ，点 $E$ 是 $C D$ 的中点，连接 $A E$ 、 $B E$ ， $∠ E A D = ∠ E A B$ ，给出下列五个结论：① $B E ⊥ A E$ ；② $B E$ 平分 $∠ A B C$ ；③ $A D + B C = A B$ ；④ $A B ⊥ B C$ ；⑤ $S_{△ A B E} = \frac{1}{2}$ S_四边形_ABCD ，其中正确的有（）

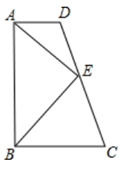A、3个 B、2个 C、5个 D、4个

查看试题解析
8. 如图，锐角△ABC 中，D 、E 分别是 AB 、AC 边上的点，△ADC≌△ADC'，△AEB≌△AEB' ，且C'D∥EB'∥BC ， BE 、CD 交于点 F ，若∠BAC = α， ∠BFC = β，则（）

A、2α+β= 180° B、2β-α= 145° C、α+β= 135° D、β-α= 60°

查看试题解析

二、填空题

9. 如图，若 $△ A B D ≌ △ A C E$ ，且 $∠ 1 = 45 °$ ， $∠ A D B = 95 °$ ，则 $∠ B =$ °.

查看试题解析
10. 三个全等三角形摆成如图所示的形式，则 $∠ α + ∠ β + ∠ γ$ 的度数为.

查看试题解析
11. 如图，若 $△ A B C ≌ △ D E F$ ， $A C = 4$ ， $A B = 3$ ， $E F = 5$ ，则 $△ A B C$ 的周长为．

查看试题解析
12. 如图，在△ABC中，AB＝AC＝24厘米，∠B=∠C ，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为厘米/秒时，能够在某一时刻使△BPD与△CQP全等．

查看试题解析
13. 如图，∠A＝∠B＝90°，AB＝60，E，F 分别为线段 AB 和射线 BD 上的一点，若点 E 从点 B 出发向点 A 运动，同时点 F 从点 B 出发向点 D 运动，二者速度之比为 3：7，运动到某时刻同时停止，在射线 AC 上取一点 G，使△AEG 与△BEF 全等，则 AG 的长为.

查看试题解析

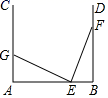
三、解答题

14. 如图，已知 $△ A B C ≌ △ D B E$ ，点D在 $A C$ 上， $B C$ 与 $D E$ 交于点P．若 $∠ A B E = 160 °$ ， $∠ D B C = 30 °$ ，求 $∠ C B E$ 的度数．

查看试题解析
15. 如图，△ABE≌△DCE，点A，C，B在一条直线上，∠AED和∠BEC相等吗？为什么？

查看试题解析

四、综合题

16. 在Rt△ABC中，AB=AC，∠BAC=90°，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到线段AE．

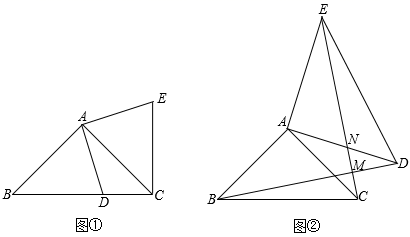(1)、探索：连接EC，如图①，试探索线段BC，CD，CE之间满足的等量关系，并证明结论；

(2)、如图②，在四边形ABCD中，∠ABC=∠ACB=45°，若BD=7，将边AD绕点A逆时针旋转90°得到线段AE．连接DE、CE，求线段CE的长．

(3)、AD与CE交于点N，BD与CE交于点M，在（2）的条件下，试探究BD与CE的位置关系，并加以证明

查看试题解析
17. 如图，在 $△ A B C$ 中， $B C = 8$ cm， $A G // B C$ ， $A G = 8$ cm，点F从点B出发，沿线段 $B C$ 以4cm/s的速度连续做往返运动，点E从点A出发沿线段 $A G$ 以2cm/s的速度运动至点G，E、F两点同时出发，当点E到达点G时，E、F两点同时停止运动， $E F$ 与 $A C$ 交于点D，设点E的运动时间为t（秒）

(1)、分别写出当 $0 < t < 2$ 和 $2 < t < 4$ 时线段 $B F$ 的长度（用含t的代数式表示）

(2)、当 $B F = A E$ 时，求t的值；

(3)、当 $△ A D E ≌ △ C D F$ 时，直接写出所有满足条件的 $t$ 值.

查看试题解析
18.

(1)、问题背景：如图1，在四边形 $A B C D$ 中， $∠ B A D = 90 °$ ， $∠ B C D = 90 °$ ， $B A = B C$ ， $∠ A B C = 120 °$ ， $∠ M B N = 60 °$ ， $∠ M B N$ 绕B点旋转，它的两边分别交 $A D$ 、 $D C$ 于E、F.探究图中线段 $A E$ ， $C F$ ， $E F$ 之间的数量关系.小李同学探究此问题的方法是：延长 $F C$ 到G，使 $C G = A E$ ，连接 $B G$ ，先证明 $△ B C G ≌ △ B A E$ ，再证明 $△ B F C ≌ △ B F E$ ，可得出结论，他的结论就是；

(2)、探究延伸1：如图2，在四边形 $A B C D$ 中， $∠ B A D = 90 °$ ， $∠ B C D = 90 °$ ， $B A = B C$ ， $∠ A B C = 2 ∠ M B N$ ， $∠ M B N$ 绕B点旋转，它的两边分别交 $A D$ 、 $D C$ 于E、F.上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由.

(3)、探究延伸2：如图3，在四边形 $A B C D$ 中， $B A = B C$ ， $∠ B A D + ∠ B C D = 180 °$ ， $∠ A B C = 2 ∠ M B N$ ， $∠ M B N$ 绕B点旋转，它的两边分别交 $A D$ 、 $D C$ 于E、F.上述结论是否仍然成立？并说明理由.

(4)、实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西 $30 °$ 的A处舰艇乙在指挥中心南偏东 $70 °$ 的B处，并且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以75海里/小时的速度前进，同时舰艇乙沿北偏东 $50 °$ 的方向以100海里/小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处，且指挥中心观测两舰艇视线之间的夹角为 $70 °$ ，试求此时两舰艇之间的距离.

查看试题解析

2023-2024学年初中数学八年级上册 13.2 全等图形 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 13.2 全等图形同步分层训练培优卷(冀教版)