2023-2024学年初中数学八年级上册 12.5 分式方程的应用同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 根据规划设计，某工程队准备修建一条长1120米的盲道．由于情况改变，实际每天修建盲道的长度比原计划增加10米，结果提前2天完成了这一任务，假设原计划每天修建盲道 $x$ 米，根据题意可列方程为（）

A、 $\frac{1120}{x} - \frac{1120}{x + 10} = 2$ B、 $\frac{1120}{x} - \frac{1120}{x - 10} = 2$ C、 $\frac{1120}{x + 10} - \frac{1120}{x} = 2$ D、 $\frac{1120}{x - 10} - \frac{1120}{x} = 2$

查看试题解析
2. $《$ 千里江山图 $》$ 是宋代王希孟的作品，如图，它的局部画面装裱前是一个长为 $2.4$ 米，宽为 $1.4$ 米的矩形，装裱后，整幅图画宽与长的比是 $8$ ： $13$ ，且四周边衬的宽度相等，则边衬的宽度应是多少米？设边衬的宽度为 $x$ 米，根据题意可列方程（）

A、 $\frac{1.4 - x}{2.4 - x} = \frac{8}{13}$ B、 $\frac{1.4 + x}{2.4 + x} = \frac{8}{13}$ C、 $\frac{1.4 - 2 x}{2.4 - 2 x} = \frac{8}{13}$ D、 $\frac{1.4 + 2 x}{2.4 + 2 x} = \frac{8}{13}$

查看试题解析
3. 某校八年级学生去距离学校 $120 k m$ 的游览区游览，一部分学生乘慢车先行，出发 $1 h$ 后，另一部分学生乘快车前往，结果他们同时到达．已知快车的速度是慢车速度的 $1.5$ 倍，求慢车的速度，设慢车的速度是 $x k m / h$ ，所列方程正确的是（）

A、 $\frac{120}{x} + 1 = \frac{120}{1.5 x}$ B、 $\frac{120}{x} - 1 = \frac{120}{1.5 x}$ C、 $\frac{120}{1.5 x} = \frac{120}{x - 1}$ D、 $\frac{120}{1.5 x} = \frac{120}{x + 1}$

查看试题解析
4. 从温州轨道交通 $S_{1}$ 线惠民路站到动车南站， $S_{1}$ 线车程约12千米，自驾车车程约15千米.小明乘坐 $S_{1}$ 线比自驾车平均速度提高了15%，时间缩短了0.1小时.设小明自驾车平均速度为每小时x千米，则下列方程正确的是（）

A、 $\frac{15}{(1 + 15 %) x} - \frac{12}{x} = 0.1$ B、 $\frac{12}{(1 + 15 %) x} - \frac{15}{x} = 0.1$ C、 $\frac{15}{x} - \frac{12}{(1 + 15 %) x} = 0.1$ D、 $\frac{12}{x} - \frac{15}{(1 + 15 %) x} = 0.1$

查看试题解析
5. 某校组织九年级学生赴韶山开展研学活动，已知学校离韶山50千米，师生乘大巴车前往，某老师因有事情，推迟了10分钟出发，自驾小车以大巴车速度的 $1.2$ 倍前往，结果同时到达．设大巴车的平均速度为x千米/时，则可列方程为（）

A、 $\frac{50}{x} = \frac{50}{1.2 x} + \frac{1}{6}$ B、 $\frac{50}{x} + 10 = \frac{50}{1.2 x}$ C、 $\frac{50}{x} = \frac{50}{1.2 x} + 10$ D、 $\frac{50}{x} + \frac{1}{6} = \frac{50}{1.2 x}$

查看试题解析
6. 某运输公司运输一批货物，已知大货车比小货车每辆多运输5吨货物，且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同，设有大货车每辆运输x吨，则所列方程正确的是（）.

A、 $\frac{75}{x - 5} = \frac{50}{x}$ B、 $\frac{75}{x} = \frac{50}{x - 5}$ C、 $\frac{75}{x + 5} = \frac{50}{x}$ D、 $\frac{75}{x} = \frac{50}{x + 5}$

查看试题解析
7. 商家常将单价不同的A，B两种糖混合成“什锦糖”出售，记“什锦糖”的单价为：A，B两种糖的总价与A，B两种糖的总质量的比．现有两种“什锦糖”：一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖”甲，另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖”乙．若B种糖比A种糖的单价贵40元/千克，“什锦糖”甲比“什锦糖”乙的单价贵5元/千克，则A种糖的单价为（）

A、50元/千克 B、60元/千克 C、70元/千克 D、80元/千克

查看试题解析
8. 张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+ $\frac{1}{x}$ （x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是 $\frac{1}{x}$ ，矩形的周长是2（x+ $\frac{1}{x}$ ）；当矩形成为正方形时，就有x= $\frac{1}{x}$ （0＞0），解得x=1，这时矩形的周长2（x+ $\frac{1}{x}$ ）=4最小，因此x+ $\frac{1}{x}$ （x＞0）的最小值是2．模仿张华的推导，你求得式子 $\frac{x^{2} + 9}{x}$ （x＞0）的最小值是（）

A、2 B、1 C、6 D、10

查看试题解析

二、填空题

9. 已知关于x的分式方程 $\frac{m - 1}{x + 1} = 1$ 的解是负数，则m的取值范围为.

查看试题解析
10. 代数式 $\frac{2}{x - 4}$ 与代数式 $\frac{3}{x - 8}$ 的值相等，则 $x =$ ．

查看试题解析
11. 甲计划用若干个工作日完成某项工作，从第三个工作日起，乙加入此项工作，且甲乙两人工效率相同，结果提前 $4$ 天完成任务，则甲计划完成此项工作的天数是．

查看试题解析
12. 甲、乙二人从同一地点同时出发沿相同路线去往同一目的地，甲一半路程以速度a行驶，一半路程以速度b行驶；乙一半时间乙速度a行驶，一半时间乙速度b行驶，问谁先到达目的地？（ $a \neq b$ ）下列结论：①甲先到；②乙先到；③甲、乙同时到达；④无法判断.
其中正确的结论是．（只需填入序号）

查看试题解析
13. 某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件，出发几分钟后，该公司快递员乙发现甲的手机落在公司，于是立马匀速骑车去追赶甲，乙出发几分钟后，甲也发现自己的手机落在了公司，立即调头以原速的2倍原路返回，1分钟后遇到了乙，乙把手机给甲后，乙以原速的一半原路返回公司，甲以返回时的速度继续去小区取物件，刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示（给手机及中途其它耽误时间忽略不计），则甲到小区时，乙距公司的路程是米.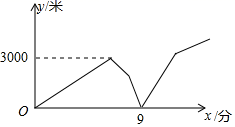

查看试题解析

三、解答题

14. 市政府为残疾人办实事，在某一道路改造工程中，为盲人修建一条长3000米的盲道，根据规划设计和要求，该市工程队在实际施工时增加了施工人员，每天修建的盲道比原计划增加了 $50 %$ ，结果提前2天完成工程．问实际每天修建盲道多少米？

查看试题解析

四、综合题

15. 一艘轮船在甲、乙两地之间匀速航行，从甲地到乙地顺流航行用 $6$ 小时，从乙地到甲地逆流航行用 $10$ 小时 $.$ 已知当时平均水流速度为每小时 $4$ 千米．

(1)、求该轮船在静水中的速度及甲乙两地的距离；

(2)、若在甲、乙两地之间的丙地新建一个码头，使该轮船从甲地匀速航行到丙地和从乙地匀速航行到丙地所用的航行时间相同 $($ 其中轮船的静水速度不变 $)$ ，问甲、丙两地相距多少千米？

查看试题解析
16. 某店3月份采购A，B两种品牌的T恤衫，若购A款40件，B款60件需进价8400元；若购A款45件，B款50件需进价8050元.

(1)、商店3月份的进货金额只有10000元，能否同时购进A款和B款T恤衫各60件？

(2)、根据3月份的销售情况，商店决定4月份和5月份均只销售A款T恤衫，4月份每件的进价比3月份涨了a元，进价合计9800元；5月份每件的进价比4月份又涨了0.5a元，进价合计12240元，数量是4月份的1.2倍.这两批A款T恤衫开始都以每件150元的价格出售，到6月初，商店把剩下的30件打八折出售，很快便售完，问商店销售这两批A款T恤衫共获毛利润（销售收入减去进价总计）多少元？

查看试题解析

2023-2024学年初中数学八年级上册 12.5 分式方程的应用 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 12.5 分式方程的应用同步分层训练培优卷(冀教版)