2023-2024学年初中数学八年级上册 12.1 分式同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 若分式 $\frac{x - 1}{x + 1}$ 的值为0，则 $x =$ （）

A、 $- 1$ B、1 C、 $\pm 1$ D、0

查看试题解析
2. 若把分式 $\frac{3 x y}{x + y}$ 中 $x$ 和 $y$ 的值都扩大为原来的 $2$ 倍，则分式的值（）

A、扩大为原来的 $2$ 倍 B、缩小为原来的 $\frac{1}{2}$ C、缩小为原来的 $\frac{1}{4}$ D、扩大为原来的 $4$ 倍

查看试题解析
3. 将分式 $\frac{x^{2} y}{x - y}$ 中的 $x$ ， $y$ 的值同时扩大为原来的 $3$ 倍，则分式的值（）

A、扩大为原来的 $6$ 倍 B、扩大为原来的 $9$ 倍 C、不变 D、扩大为原来的 $3$ 倍

查看试题解析
4. 下列各式从左往右变形正确的是（）

A、 $\frac{a}{b + 2} = \frac{a}{b}$ B、 $\frac{a}{b} = \frac{a^{2}}{b^{2}}$ C、 $\frac{a}{b} = \frac{a - 3}{b - 3}$ D、 $\frac{a}{b} = \frac{\frac{1}{3} a}{\frac{1}{3} b}$

查看试题解析
5. 如果把分式 $\frac{3 x}{x^{2} + y^{2}}$ 中的x和y都扩大3倍，那么分式的值（）

A、扩大9倍 B、扩大3倍 C、不变 D、缩小3倍

查看试题解析
6. 对于非负整数x，使得 $\frac{x^{2} + 3}{x + 3}$ 是一个正整数，则符合条件x的个数有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
7. 关于x ， y的方程xy﹣x+y＝﹣3的整数解（x ， y）的对数为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 若 $\frac{1}{2 y^{2} + 3 y + 7}$ 的值为 $\frac{1}{8}$ ，则 $\frac{1}{4 y^{2} + 6 y - 9}$ 的值是（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{17}$ C、 $- \frac{1}{7}$ D、 $\frac{1}{7}$

查看试题解析

二、填空题

9. 若分式 $\frac{x + 3}{x^{2} - 9}$ 有意义，则 $x$ 应满足的条件是．

查看试题解析
10. 若分式 $\frac{x^{2} - 4}{x + 1}$ 的值为0，则x的值为.

查看试题解析
11. 若 $a^{3} + 3 a^{2} + a = 0$ ，则 $\frac{2022 a^{2}}{a^{4} + 2015 a^{2} + 1} =$ ．

查看试题解析
12. 某段高速公路全长280公里，交警部门在高速公路上距入口3千米处设立了限速标志牌，并在以后每隔5公里处设置一块限速标志牌；此外交警部门还在距离入口10千米处设置了摄像头，并在以后每隔16千米处都设置一个摄像头（如图），则在此段高速公路上，离入口千米处刚好同时设置有标志牌和摄像头．

查看试题解析
13. 如图，在长方形ABCD中，AB=10，BC=13．E，F，G，H分别是线段AB，BC，CD，AD上的定点．现分别以BE，BF为边作长方形BEQF，以DG为边作正方形DGIH．若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形，且BE=DG，Q，I均在长方形ABCD内部．记图中的阴影部分面积分别为S₁ ， S₂ ， S₃ ．若 $\frac{S_{2}}{S_{1}} = \frac{3}{7}$ ，则S₃= ．

查看试题解析

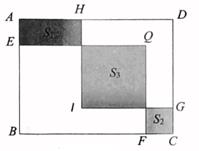
三、解答题

14. 综艺类节目《奔跑吧》火爆荧幕﹐给观众带来激情和欢乐的同时，也启示我们，团队合作、互助友爱是成功的重要因素，瞧!“撕名牌”游戏正在火热进行，下列“名牌”上的分式中，哪些是最简分式，哪些不是最简分式?如果不是最简分式，请你将其化成最简分式.

查看试题解析
15. 已知实数a，b，c满足 $a + b + c = 0$ ， $a^{2} + b^{2} + c^{2} = 1$ ，求 $(a^{5} + b^{5} + c^{5}) \div a b c$ 的值.

查看试题解析

四、综合题

16. 阅读下列材料，解答下面的问题：
我们知道方程2x+3y=12有无数个解，但在实际生活中我们往往只需求出其正整数解．

例：由2x+3y=12，得：y= $\frac{12 - 2 x}{3}$ ，根据x、y为正整数，运用尝试法可以知道方程2x+3y=12的正整数解为 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ．问题：

(1)、请你直接写出方程3x﹣y=6的一组正整数解．

(2)、若 $\frac{12}{x - 3}$ 为自然数，则满足条件的正整数x的值有（）个．

A、5 B、6 C、7 D、8

(3)、2020－2021学年七年级某班为了奖励学生学习的进步，购买单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费48元，问有哪几种购买方案？

查看试题解析
17. 我们知道，假分数可以化为整数与真分数的和的形式，例如： $\frac{3}{2} = 1 + \frac{1}{2}$ ，在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．
例如： $\frac{x + 1}{x - 2}$ ， $\frac{x^{2}}{x + 2} \cdot \cdot \cdot \cdot \cdot$ 像这样的分式是假分式；像 $\frac{1}{x - 2}$ ， $\frac{x}{x^{2} - 1} \cdot \cdot \cdot \cdot \cdot$ 这样的分式是真分式，类似的，假分式也可以化为整式与真分式的和的形式．例如： $\frac{x + 1}{x - 2} = \frac{(x - 2) + 3}{x - 2} = 1 + \frac{3}{x - 2}$ ； $\frac{x^{2}}{x + 2} = \frac{(x + 2) (x - 2) + 4}{x + 2} = x - 2 + \frac{4}{x + 2}$ ，解决下列问题：

(1)、将分式 $\frac{x - 2}{x + 3}$ 化为整式与真分式的和的形式为：（直接写出结果即可）

(2)、如果分式 $\frac{x^{2} + 2 x}{x + 3}$ 的值为整数，求 $x$ 的整数值

查看试题解析

2023-2024学年初中数学八年级上册 12.1 分式 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 12.1 分式同步分层训练培优卷(冀教版)