2023-2024学年初中数学七年级上册 2.1 从生活中认识几何图形 同步分层训练基础卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 如图所示图形中为圆柱的是( )A、
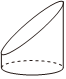 B、
B、 C、
C、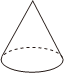 D、
D、 2. 下列各选项中的图形,绕虚线旋转一周,所得的几何体是圆锥的是( )A、
2. 下列各选项中的图形,绕虚线旋转一周,所得的几何体是圆锥的是( )A、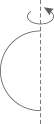 B、
B、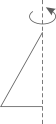 C、
C、 D、
D、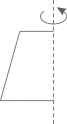 3. 如图是一个花瓶,下列平面图形绕虚线旋转一周,能形成这个花瓶表面的是( )
3. 如图是一个花瓶,下列平面图形绕虚线旋转一周,能形成这个花瓶表面的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下面四个立体图形中,和其他三个立体图形不同类的是( )A、
4. 下面四个立体图形中,和其他三个立体图形不同类的是( )A、 B、
B、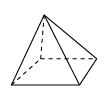 C、
C、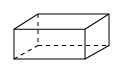 D、
D、 5. 下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )A、直角三角形 B、等腰三角形 C、矩形 D、扇形6. 在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )A、12π B、15π C、20π D、24π7. 如图,用黑板擦擦黑板时,留下的痕迹是( )
5. 下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )A、直角三角形 B、等腰三角形 C、矩形 D、扇形6. 在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )A、12π B、15π C、20π D、24π7. 如图,用黑板擦擦黑板时,留下的痕迹是( ) A、点 B、线 C、面 D、体8. “十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( )
A、点 B、线 C、面 D、体8. “十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( ) A、圆锥 B、圆柱 C、球 D、圆台
A、圆锥 B、圆柱 C、球 D、圆台二、填空题
-
9. 钟表上的时针转动一周形成一个圆面,这说明了 .10. 图中的大矩形长8厘米、宽6厘米,小矩形长4厘米、宽3厘米,以长边中点连线(图中的虚线)为轴,将图中的阴影部分旋转一周得到的几何体的表面积为平方厘米.
 11. 夏天的夜晚,萤火虫飞过,在夜空中划出一条线,这蕴含的数学原理是 .12. 10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2 .
11. 夏天的夜晚,萤火虫飞过,在夜空中划出一条线,这蕴含的数学原理是 .12. 10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2 . 13. 一位画家把7个边长为1m的相同正方体摆成如图的形状,然后把露出的表面(不包括底面)涂上颜色,则涂色面积为m2.
13. 一位画家把7个边长为1m的相同正方体摆成如图的形状,然后把露出的表面(不包括底面)涂上颜色,则涂色面积为m2.
三、综合题
-
14. 数学学习小组的同学共同探究体积为330mL圆柱形有盖容器(如图所示)的设计方案.,他们想探究容器表面积与底面半径的关系.

具体研究过程如下,请补充完整:
⑴建立模型:设该容器的表面积为S , 底面半径为cm,高为cm,则
, ①
, ②
由①式得 , 代入②式得
. ③
可知,S是x的函数,自变量x的取值范围是 .
⑵探究函数:
根据函数解析式③,按照下表中自变量x的值计算(精确到个位),得到了S与x的几组对应值:
…
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
…
…
666
454
355
303
277
266
266
274
289
310
336
…
在下面平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

⑶解决问题:根据图表回答,
①半径为2.4cm的圆柱形容器比半径为4.4cm的圆柱形容器表面积 . (填“大”或“小”);
②若容器的表面积为300 , 容器底面半径约为cm(精确到0.1).
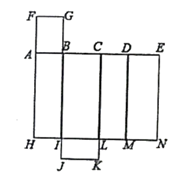
15. 如图,是底面为正方形的长方体的表面展开图,折叠成一个长方体,那么: (1)、与N重合的点是哪几个?(2)、若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?
(1)、与N重合的点是哪几个?(2)、若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?四、解答题