2023-2024学年初中数学七年级上册 5.3 解一元一次方程同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图①，约定：上方相邻两数之和等于这两数下方箭头共同指向的数．示例：即 $12 + 3 = 15$ ．如图②，当 $y = 505$ 时， $b$ 的值为（）

A、 $205$ B、 $305$ C、 $255$ D、 $315$

查看试题解析
2. 方程 $x + 3 = 2$ 的解是（）

A、 $x = 2$ B、 $x = 0$ C、 $x = - 1$ D、 $x = - 2$

查看试题解析
3. 在解方程 $\frac{x - 1}{3} + x = \frac{3 x + 1}{2}$ 时，方程两边同时乘以 $6$ ，正确的是（）．

A、 $2 x - 1 + 6 x = 9 x + 1$ B、 $2 (x - 1) + 6 x = 3 (3 x + 1)$ C、 $2 (x - 1) + x = 3 (3 x + 1)$ D、 $(x - 1) + x = 3 (3 x + 1)$

查看试题解析
4. 解方程 $\frac{x + 1}{3} - \frac{x - 1}{6} = 1$ 需下列四步，其中开始发生错误的一步是（）

A、去分母，得2（x+1）-（x-1）＝6 B、去括号，得2x+2-x+1＝6 C、移项，得2x-x＝6-2+1 D、合并同类项，得x＝5

查看试题解析
5. 方程 $- 3 (★ - 9) = 5 x - 1$ ， ★处被盖住了一个数字，已知方程的解是 $x = 2$ ，那么★处的数字是（）

A、6 B、5 C、4 D、3

查看试题解析
6. 如图，AB=30，C为射线AB上一点，BC比AC的4倍少20，P、Q两点分别从AB两点同时出发分别以2单位/秒和l单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：①BC=2AC；②运动过程中，QM的长度保持不变；③AB=4NQ；④当BQ=PB时，t=12.其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 方程|x+1|+|x-3|=4的整数解有（）

A、2个 B、3个 C、5个 D、无穷多个

查看试题解析
8. 若不论 $k$ 取什么实数，关于 $x$ 的方程 $\frac{2 k x + a}{3} - \frac{x - b k}{6} = 1$ （ $a$ 、 $b$ 常数）的解总是 $x = 1$ ，则 $a + b$ 的值是（）

A、 $- 0.5$ B、 $0.5$ C、 $- 1.5$ D、 $1$

查看试题解析

二、填空题

9. 若 $x = - 3$ 是关于x的方程 $2 x - a + 2 b = 0$ 的解，则代数式 $2 a - 4 b + 1$ 的值为．

查看试题解析
10. 若 $a ， b$ 是一元二次方程 $x^{2} - 5 x - 2 = 0$ 的两个实数根，则 $\frac{a^{3} + a^{2} b}{5 a + 2}$ 的值为．

查看试题解析
11. 在平面直角坐标系xOy中，给出如下定义：点A到x轴、y轴距离的较大值，称为点A的“长距”，当点P的“长距”等于点Q的“长距”时，称P，Q两点为“等距点”，若P（-1，4），Q（k+3，4k-3）两点为“等距点”，则k的值为．

查看试题解析
12. 若 $| a - 3 | + | a + 2 | = 6$ ，则a= ．

查看试题解析
13. 同学们都知道，|5﹣（﹣2）|表示5与﹣2之差的绝对值，实际上也可以理解为5与﹣2两数在数轴上所对应的两点之间的距离，则使得|x﹣1|+|x+5|＝6这样的整数x有个．

查看试题解析

三、解答题

14. 小英解不等式 $\frac{1 + x}{2} - \frac{2 x + 1}{3} \leq 1$ 的过程如下，请指出她解答过程中错误步骤的序号，并写出正确的解答过程.
解：去分母得： $3 (1 + x) - 2 (2 x + 1) \leq 1$ ①
去括号得： $3 + 3 x - 4 x + 1 \leq 1$ ②
移项得： $3 x - 4 x \leq 1 - 3 - 1$ ③
合并同类项得： $- x \leq - 3$ ④
两边都除以-1得： $x \leq 3$ ⑤

查看试题解析
15. 以下是圆圆解方程 $\frac{2 x - 1}{5} - \frac{x + 1}{2} = 1$ 的解答过程.
解：去分母，得 $2 (2 x - 1) - 5 (x + 1) = 10$ ……①
去括号，得 $4 x - 2 - 5 x + 5 = 10$ ……②
移项，合并同类项，得 $- x = 13$ ……③
系数化为1，得 $x = - 13$ ……④
圆圆的解答是否有错误？如果有错误，请写出正确的解答过程.

查看试题解析

四、综合题

16. 如图，有两条线段， $A B = 2$ （单位长度）， $C D = 1$ （单位长度）在数轴上，点A在数轴上表示的数是 $- 12$ ，点D在数轴上表示的数是15．

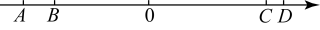(1)、点B在数轴上表示的数是，点C在数轴上表示的数是；

(2)、若线段 $A B$ 以1个单位长度/秒的速度向左匀速运动，同时线段 $C D$ 以2个单位长度秒的速度也向左匀速运动，设运动时间为t秒，当t为何值时，点B与点C之间的距离为1个单位长度？

(3)、若线段 $A B$ 、线段 $C D$ 分别以1个单位长度/秒、2个单位长度/秒的速度同时向左匀速运动，与此同时，动点P从 $- 15$ 出发，以4个单位长度/秒的速度向右匀速运动．设运动时间为t秒，当 $0 < t < 5$ 时， $2 A C - \frac{1}{3} P D$ 的值是否发生变化？若不变化，求出这个定值，若变化，请说明理由．

查看试题解析
17. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础.
例如：从“形”的角度看： $| 3 - 1 |$ 可以理解为数轴上表示 3 和 1 的两点之间的距离； $| 3 + 1 |$ 可以理解为数轴上表示 3 与-1 的两点之间的距离.
从“数”的角度看：数轴上表示 4 和-3 的两点之间的距离可用代数式表示为： 4-（-3） .

根据以上阅读材料探索下列问题：

(1)、数轴上表示 3 和 9 的两点之间的距离是；数轴上表示 2 和-5 的两点之间的距离是；（直接写出最终结果）

(2)、①若数轴上表示的数 x 和-2 的两点之间的距离是 4，则 x 的值为；
②若 x 为数轴上某动点表示的数，则式子 $| x + 1 | + | x - 3 |$ 的最小值为.

查看试题解析
18. 阅读理解：在解形如 $3 | x - 2 | = | x - 2 | + 4$ 这类含有绝对值的方程时，
解法一：我们可以运用整体思想来解.移项得 $3 | x - 2 | - | x - 2 | = 4$ ， $2 | x - 2 | = 4$ ，
$| x - 2 | = 2$ ， $x - 2 = \pm 2$ ， $x = 4$ 或 $x = 0$ .
解法二：运用分类讨论的思想，根据绝对值的意义分 $x < 2$ 和 $x \geq 2$ 两种情况讨论：
①当 $x < 2$ 时，原方程可化为 $- 3 (x - 2) = - (x - 2) + 4$ ，解得 $x = 0$ ，符合 $x < 2$ ；
②当 $x \geq 2$ 时，原方程可化为 $3 (x - 2) = (x - 2) + 4$ ，解得 $x = 4$ ，符合 $x \geq 2$ .
$∴$ 原方程的解为 $x = 0$ 或 $x = 4$ .
解题回顾：本解法中2为 $x - 2$ 的零点，它把数轴上的点所对应的数分成了 $x < 2$ 和 $x \geq 2$ 两部分，所以分 $x < 2$ 和 $x \geq 2$ 两种情况讨论.
问题：结合上面阅读材料，解下列方程：

(1)、解方程： $| x - 3 | + 8 = 3 | x - 3 |$

(2)、解方程： $| 2 - x | - 3 | x + 1 | = x - 9$

查看试题解析

2023-2024学年初中数学七年级上册 5.3 解一元一次方程 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册 5.3 解一元一次方程同步分层训练培优卷(冀教版)