2023-2024学年初中数学七年级上册 5.1 一元一次方程同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 学校组织植树活动，已知在甲处植树的有48人，在乙处植树的有42人，由于甲处植树任务较重，需调配部分乙处的人员去甲处支援，使在甲处植树的人数是乙处植树人数的2倍，设从乙处调配x人去甲处，则（　　）

A、48＝2（42-x） B、48+x＝2×42 C、48-x＝2（42+x） D、48+x＝2（42-x）

查看试题解析
2. 如果方程 $x^{2 n - 5} - 2 = 0$ 是关于x的一元一次方程，则n的值为（）

A、2 B、3 C、4 D、5

查看试题解析
3. 已知方程 $(m - 2) x^{| m | - 1} + 7 = 0$ 是关于x的一元一次方程，则 $m =$ （　　）

A、2 B、 $\pm 1$ C、 $- 2$ D、 $\pm 2$

查看试题解析
4. 元朝朱世杰所著的《算学启蒙》中，记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？其大意是：快马每天行240里，慢马每天行150里，慢马先行12天，快马几天可追上慢马？若设快马 $x$ 天可追上慢马，由题意得（）

A、 $\frac{x}{240} = \frac{x + 12}{150}$ B、 $\frac{x}{240} = \frac{x}{150} - 12$ C、 $240 (x - 12) = 150 x$ D、 $240 x = 150 (x + 12)$

查看试题解析
5. 下列说法：
①符号相反的数互为相反数；②有理数a、b、c满足 $| a + b + c | = a - b + c$ ，且 $b \neq 0$ ，则化简 $| a - 1 + c | + | b - 3 | - | b - 1 |$ 的值为5；③若 $(m - 2) x^{m^{2} - 3} + x + 2 = m$ 是关于x的一元一次方程，则这个方程的解是 $x = \frac{4}{3}$ ；④若 $(3 a + 4 b) x^{2} + a x + b = 0$ 是关于x的一元一次方程，则 $x = \frac{3}{4}$ ；

其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 如果甲、乙、丙三个村合修一段水渠,计划出工65人,按各村受益土地面积3:4:6出工,求各村应出工的人数. ①设甲、乙、丙三村分别派3x,4x,6x人,依题意可得3x+4x+6x=65; ②设甲村派x人,依题意得x+4x+6x=65; ③设甲村派x人,依题意得x+ $\frac{4}{3}$ x+2x=65； ④设丙村派x人,依题意得3x+4x+x=65.上面所列方程中正确的是( )

A、①② B、②③ C、③④ D、①③

查看试题解析
7. 李阿姨存入银行2000元，定期一年，到期后扣除20％的利息税后得到本息和为2120元，若该种储蓄的年利率为x，那么可得方程（）

A、2000（1＋x）＝2120 B、2000（1＋x％）＝2120 C、 2000（1＋x·80％）＝2120 D、2000（1＋x·20％）＝2120

查看试题解析
8. 干墨鱼用水浸泡后，重量可增加210%，某加工单位准备为某饭店提供湿墨鱼160千克，需要多少干墨鱼做原料？用x表示干墨鱼的重量，则下列方程中正确的为（）．

A、2.1x=160 B、x+2.1x=160 C、x=2.1×60 D、x+^{$\frac{x}{2.1}$}=160

查看试题解析

二、填空题

9. 我国的《九章算术》中记载道：“今有共买物，人出八，盈三；人出七，不足四．问有几人．”大意是：今有人合伙购物，每人出 $8$ 元钱，会多 $3$ 钱；每人出 $7$ 元钱，又差 $4$ 钱，问人数有多少．设有 $x$ 人，则可列方程为：．

查看试题解析
10. 《九章算术》是中国古代一部重要的数学典籍，被视为“算经之首”．其中有这样一个问题：今有共买金，人出四百，盈三千四百；人出三百，盈三百．问人数，金价各几何？其大意是，假设合伙买金，每人出400钱，还剩余3400钱；每人出300钱，还剩余300钱．问人数，金价各是多少？如果设有x个人，根据题意所列方程为．

查看试题解析
11. 如图，小红同学编了一道数学谜题，若设“□”内的数字为x，则可列出方程为.

查看试题解析
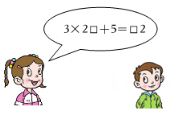12. 《莱因德纸草书》是古埃及培训年轻抄写员时可能使用的问题合集，其中记载了下列一个简单的问题：一个量与它的一半及它的三分之一加在一起变成10.若设这个量为x，则根据题意可列出方程.

查看试题解析
13. 如图，用相同的小正方形按照某种规律进行摆放，则第6个图形中小正方形的个数是，第n（n为正整数）个图形中小正方形的个数是（用含n的代数式表示）．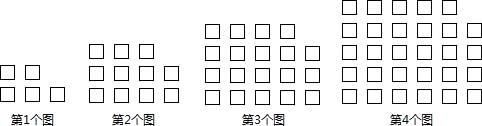

查看试题解析

三、解答题

14. 已知 $\frac{3 + a}{2}$ 与 $- \frac{1}{3} (2 a - 1) - 1$ 互为相反数，求a的值．

查看试题解析
15. 某服装商场购进一批T恤，每件进价40元，出于营销考虑，要求每件售价不得低于40元且不得高于60元，在销售过程中发现该T恤每周的销售量 $y$ （件）与每件售价 $x$ （元）之间满足一次函数关系：当销售单价为44元时，销量是72件，当销售单价为48元时，销售量为64件.

(1)、请直接写出 $y$ 与 $x$ 的函数关系式；

(2)、当商场每周销售这种T恤获得350元的利润时，每件的销售单价是多少元？

(3)、设该商场每周销售这种T恤所获得的利润为 $w$ 元，将该T恤销售单价定为多少元时，才能使商场销售该T恤所获利润最大？最大利润是多少？

查看试题解析

四、综合题

16. 一个无盖的长方体盒子的展开图如图所示．

(1)、该盒子的底面的长为（用含a的式子表示）．

(2)、若①，②，③，④四个面上分别标有整式 $2 (x + 1)$ ， x ， $- 2$ ， 4，且该盒子的相对两个面上的整式的和相等，求x的值．

(3)、请在图中补充一个长方形，使该展开图折叠成长方体盒子后有盖．

查看试题解析
17. 把四张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个长为 $m$ ，宽为 $n$ 的长方形内，该长方形内部未被卡片覆盖的部分用阴影表示.

(1)、能否用只含 $n$ 的式子表示出图②中两块阴影部分的周长和？（填“能”或“不能”）；

(2)、若能，请你用只含 $n$ 的式子表示出中两块阴影部分的周长和；若不能，请说明理由.

查看试题解析

2023-2024学年初中数学七年级上册 5.1 一元一次方程 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册 5.1 一元一次方程同步分层训练培优卷(冀教版)