2023-2024学年初中数学七年级上册 3.2 代数式同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 随着国产芯片自主研发的突破，某种型号芯片的价格经过两次降价，由原来每片a元下降到每片b元，已知第一次下降了 $10 ％$ ，第二次下降了20%，则a与b满足的数量关系是（）

A、 $b = a (1 - 10 ％ - 20 ％)$ B、 $b = a (1 - 10 ％) (1 - 20 ％)$ C、 $a = b (1 + 10 ％ + 20 ％)$ D、 $a = b (1 + 10 ％) (1 + 20 ％)$

查看试题解析
2. 某商场促销，小明将促销信息告诉了妈妈，现假设某一商品的定价为x元，小明妈妈根据信息列出了不等式 $0.8 \times (2 x - 150) < 1500$ ，那么小明告诉妈妈的信息是（）

A、买两件等值的商品可减150元，再打八折，最后不超过1500元 B、买两件等值的商品可打八折，再减150元，最后不超过1500元 C、买两件等值的商品可减150元，再打八折，最后不到1500元 D、买两件等值的商品可打八折，再减150元，最后不到1500元

查看试题解析
3. 张师傅下岗再就业，做超了小商品生意，某次进货时，他以每件a元的价格购进了20件甲种小商品，每件b元的价格购进了30件乙种小商品（ $a > b$ ）回来后，根据市场行情，他将这两种小商品都以每件 $\frac{a + b}{2}$ 元的价格出售，在这次买卖中，张师傅是（）

A、赔钱 B、赚钱 C、不赚不赔 D、无法确定赚和赔

查看试题解析
4. 如图，正方形 $A B C D$ 与正方形 $B E F G$ ，点 $C$ 在边 $B G$ 上，已知正方形 $A B C D$ 的边长 $a$ ，正方形 $B E F G$ 的边长为 $b (a < b)$ ，用 $a$ 、 $b$ 表示下列面积， $D E$ 与 $G B$ 相交于点 $H$ ，下列各选项中错误的是（）

A、 $S_{△ D A E} = S_{梯形 A B G D}$ B、 $S_{△ D H G} = S_{△ H B E}$ C、 $S_{△ D E G} = S_{正方形 A B C D}$ D、 $S_{△ D E G} = S_{△ G B E}$

查看试题解析
5. 如图，大矩形分割成五个小矩形，④号、⑤号均为正方形，其中⑤号正方形边长为1．若②号矩形的长与宽的差为2，则知道哪个小矩形的周长，就一定能算出这个大矩形的面积（）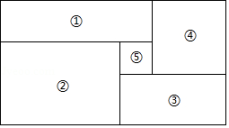

A、①或③ B、② C、④ D、以上选项都可以

查看试题解析
6. 已知我省2022年上半年的 $G D P$ 总值为 $a$ 万亿元，2022年下半年的 $G D P$ 总值比2022年上半年增长 $7.5 %$ ，预计2023年上半年的 $G D P$ 总值比2022年下半年增长 $6.8 %$ ，若预计我省2023年上半年的 $G D P$ 总值为 $b$ 万亿元，则a，b之间的关系是（）

A、 $b = (1 + 6.8 %) (1 + 7.5 %) a$ B、 $b = (1 + 7.5 %)^{2} a$ C、 $a = (1 - 6.8 %) (1 - 7.5 %) b$ D、 $b = (1 + 7.5 % + 6.8 %) a$

查看试题解析
7. 【阅读理解】计算：25×11＝275，13×11＝143，48×11＝528，74×11＝814，观察算式，我们发现两位乘11的速算方法：头尾一拉，中间相加，满十进一.
【拓展应用】已知一个两位数，十位上的数字是a，个位上的数字是b，这个两位数乘11，计算结果的十位上的数字可表示为（　　）

A、a或a＋1 B、a＋b或ab C、a＋b−10 D、a＋b或a＋b−10

查看试题解析
8. 如图所示的大长方形被分割成4个大小不同的正方形(1)(2)(4)和一个小长方形(5)，有下列结论：
（ 1 ）若已知小正方形(1)和(2)的周长，就能求出大长方形的周长；（2）若已知小正方形(3)的周长，就能求出大长方形的周长；（3）若已知小正方形(4)的周长，就能求出大长方形的周长；(4) 若已知小长方形(5)的周长，就能求出大长方形的周长。其中正确的是（）

A、(1) (2) (4) B、(1) (2) (3) C、(1) (3) D、(2) (3)

查看试题解析

二、填空题

9. 2023长春马拉松于5月21日在南岭体育场鸣枪开跑，某同学参加了7.5公里健康跑项目，他从起点开始以平均每分钟x公里的速度跑了10分钟，此时他离健康跑终点的路程为公里．（用含x的代数式表示）

查看试题解析
10. 如图所示，已知长方形ABCD的长AD=8，内有边长相等的小正方形AIGJ和小正方形ELCK，其重叠部分为长方形EFGH．设小正方形边长为a，则EH的长为(用a的代数式表示)．若长方形ABCD的宽AB=6，长方形EFGH的周长为8，则图中阴影部分周长和为．

查看试题解析
11. 任意给一个非零数 $x$ ，按下列程序写出输出结果：（写出 $y$ 与 $x$ 的关系式）．

查看试题解析
12. 有一个长方体水箱，从里面量得它的深度为 $30 c m$ ，底面长为 $25 c m$ ，宽为 $20 c m$ ，水箱里已盛有深度为 $a (c m) (a \leq 30)$ 的水.若往水箱里放入一个棱长为 $10 c m$ 的立方体铁块，则水箱的水深为 $c m$ .

查看试题解析
13. 如图，把六张形状大小完全相同的小长方形卡片（如图①）不重叠的放在一个底面为长方形（长为acm，宽为bcm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是.

查看试题解析

三、解答题

14. 底面为正方形的长方体，体积为 $32 {cm}^{3}$ ，底面边长为 $x (cm)$ ，请用含 $x$ 的式子表示这个长方体的高 $h (cm)$ ，并求当底面边长为 $2 cm$ 时 $h$ 的值.

查看试题解析
15. 某建筑物的窗户如图所示，它的上部是由4个扇形组成的半圆形，下部是由边长都为 $a$ 的4个小正方形组成的正方形，用含 $a$ 的代数式表示制造窗框的材料总长（即图中所有黑线的长度和）．

查看试题解析

四、综合题

16. 如图

(1)、【操作感知】如图①，长方形透明纸上有一条数轴， $A B$ 是周长为4的圆的直径，点 $A$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动1周，点 $A$ 落在数轴上的点 $A^{'}$ 处；将圆从原点出发沿数轴负方向滚动半周，点 $B$ 落在数轴上的点 $B^{'}$ 处，折叠长方形透明纸，使数轴上的点 $A^{'}$ 与点 $B^{'}$ 重合，此时折痕与数轴交点表示的数为.

(2)、【建立模型】折叠长方形透明纸，使得数轴上表示数 $a$ 的点 $M$ 与表示数 $b$ 的点 $N$ 重合，则折痕与数轴交点表示的数为（用含 $a$ ， $b$ 的代数式表示）.

(3)、【问题解决】若 $C$ ， $D$ ， $E$ 为数轴上不同的三点，点 $C$ 表示的数为 $4$ ，点 $D$ 表示的数为-2，如果 $C$ ， $D$ ， $E$ 三点中的一点到其余两点的距离相等，求点 $E$ 表示的数；

(4)、如图②，若 $A B$ 是周长为 $3$ 的圆的直径，点 $A$ 与数轴原点重合，将圆从原点出发沿数轴正方向滚动2周，点 $A$ 落在数轴上的点 $Q$ 处；将圆从原点出发沿数轴负方向滚动 $1$ 周，点 $A$ 落在数轴上的点 $P$ 处.将此长方形透明纸沿 $P$ ， $Q$ 剪开，将点 $P$ ， $Q$ 之间一段透明纸对折，使其左、右两端重合，这样连续对折 $n$ 次后，再将其展开，求最右端折痕与数轴交点表示的数.

查看试题解析
17. 阅读以下材料，并解答问题．
阅读一：画与三角形面积相等的长方形．

(1)、如图1，已知 $△ A B C$ ， ①画 $B C$ 边上的高 $A D$ ；②取线段 $A D$ 的中点E；③以 $B C$ 为边画长方形 $B C F G$ ，使得 $B G = C F = D E$ 那么长方形 $B C F G$ 的面积等于 $△ A B C$ 的面积．
根据“阅读一”，如果 $B C = 8 ， A D = 4$ ，那么长方形 $B C F G$ 的面积= ▲ ．
阅读二：画与长方形面积相等的正方形．
如图2，已知长方形 $B C F G$ ， ①延长 $G F$ ，截取 $F H = C F$ ；
②以 $G H$ 的中点O为圆心， $G O$ 为半径作半圆；
③过点F画 $G H$ 的垂线，交半圆于点I；④以 $F I$ 为边画正方形 $F I J K$ 那么正方形 $F I J K$ 的面积等于长方形 $B C F G$ 的面积．

(2)、根据“阅读二”，设 $G O = a ， O F = b$ ，如果等面积的正方形 $F I J K$ 边长为5，请猜想a、b的数量关系并加以说明；

(3)、根据“阅读一”由 $△ A B C$ 画出它的等面积长方形 $B C F G$ ，在长方形 $B C F G$ 的基础上，再根据“阅读二”画出等面积正方形FIJK，设 $B C = m ， A D = n$ ，当H为 $F K$ 的中点时，m、n的数量关系为：．

查看试题解析

2023-2024学年初中数学七年级上册 3.2 代数式 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学七年级上册 3.2 代数式同步分层训练培优卷(冀教版)