2023-2024学年初中数学七年级上册 2.8 平面图形的旋转 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 如图,与关于点成中心对称,连结、 , 以下结论错误的是( )
 A、 B、 C、 D、2. 如图,三角形是由三角形绕点顺时针旋转后得到的图形,则的度数是( )
A、 B、 C、 D、2. 如图,三角形是由三角形绕点顺时针旋转后得到的图形,则的度数是( ) A、 B、 C、 D、3. 在如图右侧的四个三角形中,不能由经过旋转或平移得到的是( )
A、 B、 C、 D、3. 在如图右侧的四个三角形中,不能由经过旋转或平移得到的是( ) A、 B、 C、 D、4. 下列现象:①地下水位逐年下降,②传送带的移动,③方向盘的转动,④水龙头的转动;其中属于旋转的有( )A、4个 B、3个 C、2个 D、1个5. 如图,在中, , 将绕点C按顺时针方向旋转得到 , 此时点E恰在边上,则旋转角的大小为( )
A、 B、 C、 D、4. 下列现象:①地下水位逐年下降,②传送带的移动,③方向盘的转动,④水龙头的转动;其中属于旋转的有( )A、4个 B、3个 C、2个 D、1个5. 如图,在中, , 将绕点C按顺时针方向旋转得到 , 此时点E恰在边上,则旋转角的大小为( ) A、 B、 C、 D、6. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( )
A、 B、 C、 D、6. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,则∠AOB'的度数是( ) A、25° B、30° C、35° D、40°7. 如图,在中, , 将绕点顺时针旋转得到 , 点、的对应点分别为、 , 连接 , 当、、在同一直线上时,下列结论正确的是( )
A、25° B、30° C、35° D、40°7. 如图,在中, , 将绕点顺时针旋转得到 , 点、的对应点分别为、 , 连接 , 当、、在同一直线上时,下列结论正确的是( ) A、 B、 C、 D、8. 如图,△ABC是等边三角形,AB=4,E是AC的中点,D是直线BC上一动点,线段ED绕点E逆时针旋转90°,得到线段EF,当点D运动时,则AF的最小值为( )
A、 B、 C、 D、8. 如图,△ABC是等边三角形,AB=4,E是AC的中点,D是直线BC上一动点,线段ED绕点E逆时针旋转90°,得到线段EF,当点D运动时,则AF的最小值为( )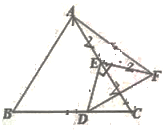 A、2 B、 C、 D、 +1
A、2 B、 C、 D、 +1二、填空题
-
9. 如图,已知中, , , 如果将绕点C顺时针旋转到 , 使点B的对应点落在边上,那么的度数是 .
 10. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=45°,∠BOD=60°,则∠BOC= .
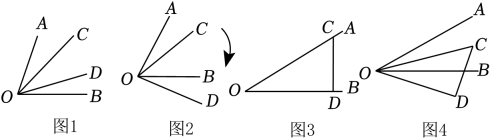
10. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=45°,∠BOD=60°,则∠BOC= . 11. 如图(1),在三角形中, , , 边绕点按逆时针方向旋转一周回到原来的位置(即旋转角),在旋转过程中(图2),当时,旋转角为度;当所在直线垂直于时,旋转角为度.
11. 如图(1),在三角形中, , , 边绕点按逆时针方向旋转一周回到原来的位置(即旋转角),在旋转过程中(图2),当时,旋转角为度;当所在直线垂直于时,旋转角为度. 12. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.
12. 如图1,一款暗插销由外壳 , 开关 , 锁芯DE三部分组成,其工作原理如图2,开关绕固定点O转动,由连接点D带动锁芯DE移动.图3为插销开启状态,此时连接点D在线段上,如位置.开关绕点O顺时针旋转180°后得到 , 锁芯弹回至位置(点B与点重合),此时插销闭合如图4.已知 , , 则mm.
 13. 如图,数轴上放置的正方形的周长为个单位,它的两个顶点A、分别与数轴上表示和的两个点重合.现将该正方形绕顶点按顺时针方向在数轴上向右无滑动的翻滚,当正方形翻滚一周后,点A落在数轴上所对应的数为 .
13. 如图,数轴上放置的正方形的周长为个单位,它的两个顶点A、分别与数轴上表示和的两个点重合.现将该正方形绕顶点按顺时针方向在数轴上向右无滑动的翻滚,当正方形翻滚一周后,点A落在数轴上所对应的数为 . (1)、当正方形翻滚三周后,点A落在数轴上所对应的数为;(2)、如此继续下去,当正方形翻滚周后表示正整数 , 用含的式子表示点A落在数轴上所对应的数为 .
(1)、当正方形翻滚三周后,点A落在数轴上所对应的数为;(2)、如此继续下去,当正方形翻滚周后表示正整数 , 用含的式子表示点A落在数轴上所对应的数为 .三、解答题
-
14. 如图,将绕点A逆时针旋转得到 . 使点B的对应点E落在边上,求的度数.
 15. 如图,逆时针旋转一定角度后与重合,且点在上.若 , , 求出旋转角的度数,并写出旋转中心.
15. 如图,逆时针旋转一定角度后与重合,且点在上.若 , , 求出旋转角的度数,并写出旋转中心.
四、综合题
-
16. 新定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.
如图1,若射线 , 在的内部,且 , 则是的内半角.
根据以上信息,解决下面的问题:
(1)、如图1, , , 若是的内半角,则 ;(2)、如图2,已知 , 将绕点按顺时针方向旋转一个角度()至.若是的内半角,求的值;(3)、把一块含有角的三角板按图3方式放置.使边与边重合,边与边重合.如图4,将三角板绕顶点以3度/秒的速度按顺时针方向旋转一周,旋转时间为秒,当射线、、、构成内半角时,直接写出的值.17. 有两个形状、大小完全相同的直角三角板ABC和CDE,其中∠ACB=∠DCE=90°.将两个直角三角板ABC和CDE如图①放置,点A,C,E在直线MN上.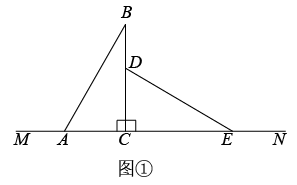
 (1)、三角板CDE位置不动,将三角板ABC绕点C顺时针旋转一周,
(1)、三角板CDE位置不动,将三角板ABC绕点C顺时针旋转一周,①在旋转过程中,若∠BCD=35°,则∠ACE= ▲ °;
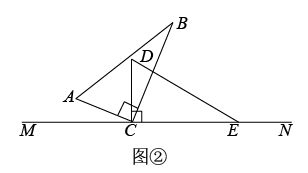
②在旋转过程中,∠BCD与∠ACE有怎样的数量关系?请依据图②说明理由.
(2)、在图①基础上,三角板ABC和CDE同时绕点C顺时针旋转,若三角板ABC的边AC从CM处开始绕点C顺时针旋转,转速为12°/秒,同时三角板CDE的边CE从CN处开始绕点C顺时针旋转,转速为2°/秒,当AC旋转一周再落到CM上时,两三角板都停止转动.如果设旋转时间为t秒,则在旋转过程中,当∠ACE=2∠BCD时,t为多少秒?