2023-2024学年初中数学七年级上册 2.6 角的大小 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 下列说法正确的有( )个
①两点确定一条直线;②两点之间,直线最短;③角的两边越长,角就越大;④若线段 , 则点B是线段的中点.
A、4个 B、3个 C、2个 D、1个2. 在同一平面内,已知 , , 则等于( ).A、80° B、40° C、80°或40° D、20°3. 下面所标注的四个角中最大的角是( )A、 B、
B、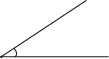 C、
C、 D、
D、 4. 图中所示的网格是正方形网格,则下列关系正确的是( )
4. 图中所示的网格是正方形网格,则下列关系正确的是( )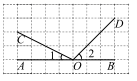 A、 B、 C、 D、5. 下列说法正确的个数是( )
A、 B、 C、 D、5. 下列说法正确的个数是( )①连接两点之间的线段叫两点间的距离
②射线有两个端点
③若AB=2CB,则点C是AB的中点
④若∠A=20°18′,∠B=20°28″,∠C=20.25°,则有∠A>∠C>∠B
A、1个 B、2个 C、3个 D、4个6. 已知∠A= ,∠B=30.45°,则∠A( )∠BA、 B、 C、= D、无法确定7. 如图, 与 之间的关系是( ) A、 B、 C、 D、 与 的大小无法比较8. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:
A、 B、 C、 D、 与 的大小无法比较8. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:已知:∠AOB
求作:∠A′O′B′,使∠A′O′B′=∠AOB
作法:⑴如图,以点O为圆心,m为半径画弧,分别交OA,OB于点C,D;
⑵画一条射线O′A′,以点O′为圆心,n为半径画弧,交O′A′于点C′;
⑶以点C′为圆心,p为半径画弧,与第(2)步中所画的弧相交于点D′;
⑷过点D′画射线O′B′,则∠A′O′B′=∠AOB.
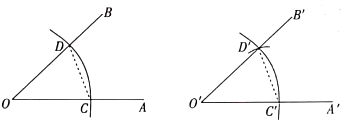
下列说法正确的是( )
A、m=p>0 B、n=p>0 C、p=n>0 D、m=n>0二、填空题
-
9. 用10倍放大镜看30°的角,你观察到的角是.10. 比较大小:18.25°18°25′(填“>”“<”或“=”)11. 比较图中、的大小:因为和是公共边,在的内部,所以 . (填“>”,“<”或“=”)
 12. 如图,将量角器的中心与的顶点重合,读出射线OA,OB分别经过刻度18和140,把绕点O顺时针方向旋转到 , 读出的平分线OC经过刻度32,则的平分线经过的刻度是 .
12. 如图,将量角器的中心与的顶点重合,读出射线OA,OB分别经过刻度18和140,把绕点O顺时针方向旋转到 , 读出的平分线OC经过刻度32,则的平分线经过的刻度是 . 13. 比较两个角 和 的大小关系:小明用度量法测得 ;小丽采用叠合法比较这两个角的大小,她将 和 的顶点重合,边 与 重合,边 和 置于重合边的同侧,则边 .(填序号:①“在 的内部”;②“在 的外部”;③“与边 重合”)
13. 比较两个角 和 的大小关系:小明用度量法测得 ;小丽采用叠合法比较这两个角的大小,她将 和 的顶点重合,边 与 重合,边 和 置于重合边的同侧,则边 .(填序号:①“在 的内部”;②“在 的外部”;③“与边 重合”)三、解答题
-
14. 如图,OC在∠BOD内.
 (1)、如果∠AOC和∠BOD都是直角.
(1)、如果∠AOC和∠BOD都是直角.①若∠BOC=60°,则∠AOD的度数是 ▲ ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)、如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.四、作图题
-
15. 如图,测绘平面上有两个点A,B.应用量角器和圆规完成下列画图或测量:

①连接AB,点C在点B北偏东30°方向上,且BC=2AB,作出点C(保留作图痕迹);
②在(1)所作图中,D为BC的中点,连接AD,AC,画出∠ADC的角平分线DE交AC于点E;
③在①②所作图中,用量角器测量∠BDE的大小(精确到度).
五、综合题
-
16. 如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.
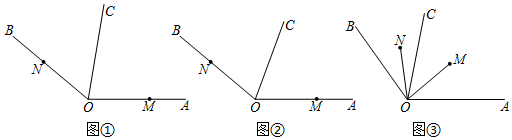 (1)、若∠AOB=140°,当t=2秒时,∠MON= , 当t=4秒时,∠MON=;(2)、如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.(3)、如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出 的值.17. 已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.
(1)、若∠AOB=140°,当t=2秒时,∠MON= , 当t=4秒时,∠MON=;(2)、如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.(3)、如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出 的值.17. 已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE. (1)、如图1所示,当∠DOE=20°时,∠FOH的度数是.(2)、若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.(3)、若再作射线OG平分∠BOF,试求∠GOH的度数.18. 已知,直线AB与直线CD相交于O,OB平分∠DOF.
(1)、如图1所示,当∠DOE=20°时,∠FOH的度数是.(2)、若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.(3)、若再作射线OG平分∠BOF,试求∠GOH的度数.18. 已知,直线AB与直线CD相交于O,OB平分∠DOF. (1)、如图,若∠BOF=40°,求∠AOC的度数;(2)、作射线OE,使得∠COE=60°,若∠BOF=x°( ),求∠AOE的度数(用含x的代数式表示).
(1)、如图,若∠BOF=40°,求∠AOC的度数;(2)、作射线OE,使得∠COE=60°,若∠BOF=x°( ),求∠AOE的度数(用含x的代数式表示).
-
-