2023-2024学年初中数学七年级上册 2.2 点和线 同步分层训练培优卷(冀教版)
试卷更新日期：2023-08-02 类型：同步测试
一、选择题
-
1. 如图，C、D两点在线段AB上，则图中共有线段（ ）条．
A、3 B、4 C、5 D、62. 如图，C、D是线段AB上的点，若AB＝8，CD＝2，则图中以A、C、D、B为端点的所有线段的长度之和为（ ）
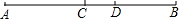A、24 B、22 C、20 D、263. 木匠在木料上画线，先确定两个点的位置，就能把线画得很准确，其依据是（ ）A、两点之间线段最短 B、过一点有无数条直线 C、两点确定一条直线 D、两点之间线段的长度叫做这两点之间的距离4. 下列叙述正确的是（ ）A、线段AB可表示为线段BA B、射线AB可表示为射线BA C、直线可以比较长短 D、射线可以比较长短5. 在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（ ）①用两颗钉子就可以把木条固定在墙上；②在砌墙前，师傅会在墙两端拉一根笔直的水平线；③把弯曲的公路改直；④植树时栽下两棵树，就可以把同一行树栽在同一条直线上．
A、①② B、①②④ C、①④ D、①②③6. 如果线段AB=13cm，MA+MB=17 cm，那么下面说法中正确的是（ ）.A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上，也可能在直线AB外7. 如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（ ）A、4cm B、2cm C、4cm或2cm D、小于或等于4cm，且大于或等于2cm8. 平面内的9条直线任两条都相交，交点数最多有m个，最少有n个，则m+n等于（ ）A、36 B、37 C、38 D、39二、填空题
-
9. 在墙壁上固定一根木条，至少要钉铁钉，理由是。10. 如图，以点О为端点的射线有条.
11. 建筑工人在砌墙时，经常在两个墙角分别立一根标志杆，在两根标志杆之间拉一条线，沿这条线就可以砌出直的墙了，其中的数学道理是 ．
12. 如图，点C，D分别为线段AB（端点A，B除外）上的两个不同的动点，点D始终在点C右侧，图中所有线段的和等于30 cm，且AB＝3CD，则CD＝cm.
13. 如图，线段AB=BC=CD=DE=1cm，图中所有线段的长度之和为cm．
三、解答题
-
14. 已知：线段m，n求作：线段AB，使 ．
15.如图，点C在线段AB上，AC=8 cm，CB=6 cm，点M、N分别是AC、BC的中点．
（1）求线段MN的长；
（2）若C为线段AB上任一点，满足AC+CB=a cm，其它条件不变，你能猜想MN的长度吗？并说明理由；
（3）若C在线段AB的延长线上，且满足AC﹣BC=bcm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由；
（4）你能用一句简洁的话，描述你发现的结论吗？
四、作图题
-
16. 图①、图②、图③均是3×3的正方形网格，每个小正方形的顶点称为格点，线段AB的端点和点P均在格点上．请按要求完成作图，保留作图痕迹．
(1)、在图①中画一条以P为端点的射线PC，使其平分线段AB，点C在线段AB上；(2)、在图②中画一条以P为端点的射线PD，使其分线段AB为1：3两部分，点D在线段AB上；(3)、在图③中画一条以P为端点的射线PE，使tan∠PEB＝1，点E在线段AB上．五、综合题
-
17.(1)、观察思考：如图，线段AB上有两个点C、D，请分别写出以点A、B、C、D为端点的线段，并计算图中共有多少条线段；
(2)、模型构建：如果线段上有m个点（包括线段的两个端点），则该线段上共有多少条线段？请说明你结论的符合题意性；(3)、拓展应用：某班45名同学在毕业后的一次聚会中，若每两人握1次手问好，那么共握多少次手？请将这个问题转化为上述模型，并直接应用上述模型的结论解决问题．
18. 如图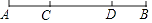
(1)、观察思考如图，线段AB上有两个点C、D，请分别写出以点A、B、C、D为端点的线段，并计算图中共有多少条线段；
(2)、模型构建如果线段上有m个点（包括线段的两个端点），则该线段上共有多少条线段？请说明你结论的正确性；
(3)、拓展应用8位同学参加班上组织的象棋比赛，比赛采用单循环制（即每两位同学之间都要进行一场比赛），那么一共要进行多少场比赛？
请将这个问题转化为上述模型，并直接应用上述模型的结论解决问题．
-