2023-2024学年初中数学七年级上册 2.1 从生活中认识几何图形 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 如图所示图形绕直线旋转一周,可以得到圆柱的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )A、直角三角形 B、等腰三角形 C、矩形 D、扇形3. 如图,用黑板擦擦黑板时,留下的痕迹是( )
2. 下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )A、直角三角形 B、等腰三角形 C、矩形 D、扇形3. 如图,用黑板擦擦黑板时,留下的痕迹是( ) A、点 B、线 C、面 D、体4. “十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( )
A、点 B、线 C、面 D、体4. “十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( ) A、圆锥 B、圆柱 C、球 D、圆台5. 用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )
A、圆锥 B、圆柱 C、球 D、圆台5. 用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )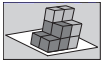 A、
A、 B、
B、 C、
C、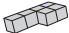 D、
D、 6. 如图所示的花瓶中, 的表面,可以看作由所给的平面图形绕虚线旋转一周形成的.
6. 如图所示的花瓶中, 的表面,可以看作由所给的平面图形绕虚线旋转一周形成的. A、
A、 B、
B、 C、
C、 D、
D、 7. 把立方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花朵的朵数情况列表如下:现将上述大小相同,颜色、花朵分布完全样的四个立方体拼成一个水平放置的长方体,如图所示,那么长方体的下底面共有花朵数是( )
7. 把立方体的六个面分别涂上六种不同的颜色,并画出朵数不等的花,各面上的颜色与花朵的朵数情况列表如下:现将上述大小相同,颜色、花朵分布完全样的四个立方体拼成一个水平放置的长方体,如图所示,那么长方体的下底面共有花朵数是( )颜色
红
黄
蓝
白
紫
绿
花朵数
1
2
3
4
5
6
 A、11 B、13 C、15 D、178. 若两个图形有公共点,则称这两个图形相交,否则称它们不相交.如图,直线PA、PB和线段AB将平面分成五个区域(不包含边界),若线段PQ与线段AB相交,则点Q落在的区域是( )
A、11 B、13 C、15 D、178. 若两个图形有公共点,则称这两个图形相交,否则称它们不相交.如图,直线PA、PB和线段AB将平面分成五个区域(不包含边界),若线段PQ与线段AB相交,则点Q落在的区域是( )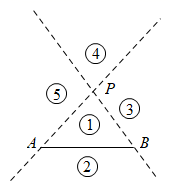 A、① B、② C、③ D、④或⑤
A、① B、② C、③ D、④或⑤二、填空题
-
9. 10个棱长为ycm的正方体摆放成如图的形状,则这个图形的表面积为 cm2 .
 10. 夏天的夜晚,萤火虫飞过,在夜空中划出一条线,这蕴含的数学原理是 .11. 如图,由18个棱长为2cm的正方体拼成的立体图形,它的表面积是cm2.
10. 夏天的夜晚,萤火虫飞过,在夜空中划出一条线,这蕴含的数学原理是 .11. 如图,由18个棱长为2cm的正方体拼成的立体图形,它的表面积是cm2.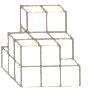 12. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.
12. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.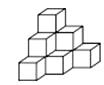 13. 一个由许多规格相同的小正方体堆积而成的几何体,其主视图、左视图如图所示一模一样,若要摆成这样的图形,至少需用 m 块小正方体,至多需用n 块小正方体,则 mn= .
13. 一个由许多规格相同的小正方体堆积而成的几何体,其主视图、左视图如图所示一模一样,若要摆成这样的图形,至少需用 m 块小正方体,至多需用n 块小正方体,则 mn= .
三、解答题
-
14.
下图是一个三角形,现分别连接这个三角形三边的中点将这个三角形分割成4个较小的三角形(即分割成四部分)得到图①,再连接中间这个三角形三边的中点继续将它分割得到图②;再继续连接最中心三角形三边的中点将它分割得到图③.
(1)图②中大三角形被分割成 个三角形;图③中大三角形被分割成 个三角形.
(2)按上面的方法继续分割下去,第10个图形分割成几个三角形?第n个图形呢(用n的代数式表示结论)?
 15.
15.如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.
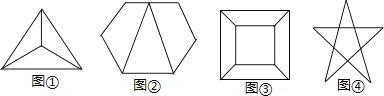
(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
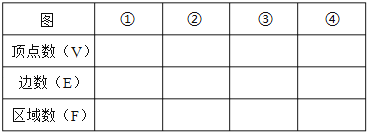
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
四、作图题
-
16. 补画长方体(用虚线表示被遮住的线段;只要在已有图形基础上画出长方体,不必写画法).

五、综合题
-
17. 如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
 (1)、拼成的正方形的面积为 , 边长为.(2)、如图2,以数轴的单位长度的线段为边作一个直角三角形,以数轴上表示 的﹣1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是 .(3)、如图3,网格中每个小正方形的边长为1,若把阴影部分剪拼成一个正方形,那么新正方形的边长是 .18. 如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)、拼成的正方形的面积为 , 边长为.(2)、如图2,以数轴的单位长度的线段为边作一个直角三角形,以数轴上表示 的﹣1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是 .(3)、如图3,网格中每个小正方形的边长为1,若把阴影部分剪拼成一个正方形,那么新正方形的边长是 .18. 如图,是由若干个完全相同的小正方体组成的一个几何体. (1)、请画出这个几何体的三视图;
(1)、请画出这个几何体的三视图;
(2)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加个小正方体.
-