2023年浙教版数学七年级上册2.1 有理数的加法同步测试（培优版）

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，将 $- 3$ ， $- 2$ ， $- 1$ ， 0，1，2，3，4，5分别填入九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在a，b，c分别表示其中的一个数，则 $a - b + c$ 的值为（）
4
a
2
$- 1$
1
3
b
5
c

A、5 B、 $- 4$ C、0 D、 $- 5$

查看试题解析
2. 已知abc>0，则式子： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为（）

A、3 B、-3或1 C、-1或3 D、1

查看试题解析
3. 把 $- 3$ ， $- 2$ ， $- 1$ ， $0$ ， $1$ 这五个数填入下列圆中，使行、列三个数的和相等，其中错误的是（）

A、 B、 C、 D、

查看试题解析
4. 设a是最小的自然数，b是最小的正整数，c是最大的负整数，则a、b、c三数的和为（）

A、3 B、2 C、1 D、0

查看试题解析
5. 已知 $| a | = 5 ， | b | = 2$ ，且 $| a - b | = b - a$ ，则 $a + b$ 的值为（）

A、3或7 B、-3或-7 C、-3或7 D、3或-7

查看试题解析
6. 已知a与b的和为2，b与c互为相反数，若 $| c | = 1$ ，则a的值为（　　）

A、1或3 B、2或-4 C、3 D、3或-3

查看试题解析
7. 在数轴上从左到右有A，B，C三点，其中AB＝1，如图所示．设点A，B，C所对应数的和是x（）

A、若以点A为原点，则x的值是4 B、若以点B为原点，则x的值是1 C、若以点C为原点，则x的值是﹣4 D、若以BC的中点为原点，则x的值是﹣2

查看试题解析
8. 在下列执行异号两数相加的步骤中，错误的是（）
①求两个有理数的绝对值；②比较两个有理数绝对值的大小；③将两个有理数绝对值的和作为结果的绝对值；④将绝对值较大数的符号作为结果的符号.

A、① B、② C、③ D、④

查看试题解析
9. 在计算 $\frac{7}{15} + (- \frac{2}{7}) + ■$ 时， $■$ 中可以填入的使该题用简便方法进行计算的数值为（）

A、 $\frac{5}{8}$ B、 $\frac{1}{6}$ C、 $\frac{7}{10}$ D、 $\frac{8}{15}$

查看试题解析
10. 将－5，－4，－3，－2，－1，0，1，2，3填入九宫格内，使每行、每列、每条斜对角线上的3个数和都相等，如图所示的x处应填（）

A、－5 B、－4 C、－3 D、－2

查看试题解析

二、填空题

11. 若 $x$ 与3互为相反数，则 $x + 4$ 等于.

查看试题解析
12. 幻方是相当古老的数学问题，我国古代的《洛书》中记载的龟背图是最早的幻方．如图所示，若将数字1~9填入这个3×3幻方中，恰好能使每一横行，每一竖列以及两条对角线上的数字之和相等，则m的值为．

查看试题解析
13. 纽约与北京的时差为-13时，小明在北京乘坐早晨8：00的航班飞行约20个小时到达纽约，那么小明到达纽约时间是.

查看试题解析
14. 已知 $| a - 1 | = 3$ ， $| b | = 5$ ，且 $| a - b | = | a | + | b |$ ，求 $a + b =$ ．

查看试题解析
15. 在1、5、 $-$ 2中任意取两个相加，其中最大的和是，最小的和是．

查看试题解析

三、计算题

16. 阅读（1）题的计算方法，再计算（2）题.
（ 1 ）计算： $(- 5 \frac{5}{6}) + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ .

解：原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{3}{4}) + [(- 3) + (- \frac{1}{2})]$

$= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})] = 0 + (- 1 \frac{1}{4}) = - 1 \frac{1}{4}$ .

上面这种解题方法叫拆项法.

（ 2 ）计算； $(- 2018 \frac{5}{6}) + (- 2017 \frac{2}{3}) + 4033 \frac{2}{3} + (- 1 \frac{1}{2})$

查看试题解析

四、综合题

17. 在一条不完整的数轴上从左到右有点 $A ， B ， C$ ，其中 $A B = 2 ， B C = 1$ ，如图所示. 设点 $A ， B ， C$ 所对应的数的和是 $m$ .

(1)、若以B为原点，写出点 $A ， C$ 所表示的数，并计算m的值.

(2)、若原点O在图中数轴上点C的右边，且点O到C的距离为28，求m的值.

查看试题解析
18. 某学习平台开展打卡集点数的活动，所获得的点数可以换学习用品和学习资料，规则如下：首日打卡领5个点数，连续打卡每日再递增5个点数，每日可领取的点数的数量最高为30个，若中断，则下次打卡作首日打卡，点数从5个开始重新领取．

(1)、按规则，第1天打卡领取5个点数，连续打卡，则第2天领取10个点数，第3天领取15个点数，第6天领取个点数，第7天领取个点数；连续打卡7天，一共领取个点数．

(2)、小红从1月1日开始打卡，连续打卡10天，一共能领取个点数；若1月6日不小心忘记打卡，则这10天会少领取个点数．

查看试题解析
19. 如图1，在 $3 \times 3$ 的九个格子中填入 $9$ 个数字，当每行、每列及每条对角线的 $3$ 个数字之和都相等时，我们把这张图称之为九宫归位图：

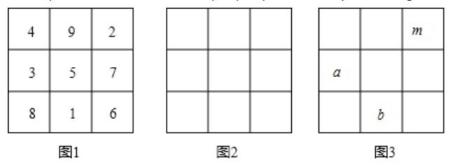(1)、若 $- 2 、 - 1 、 0 、 1 、 2 、 3 、 4 、 5 、 6$ ，这 $9$ 个数也能构成九宫归位图，则此时每行、每列及每条对角线的 $3$ 个数字之和都为；

(2)、如图2.在这张九宫归位图中，只填入了 $3$ 个数，请将剩余的 $6$ 个数直接填入表2中；(用含 $a$ 的代数式分别表示这 $6$ 个数)

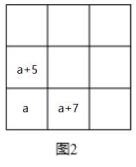(3)、如图3，在这张九宫归位图中，只填入了 $2$ 个数，请你求出右上角“ $?$ ”所表示的数值.

查看试题解析
20.

(1)、比较大小（用“ $<$ ”“ $>$ ”或“ $=$ ”填空）．
① $| + 2 | + | - 3 |$ $| (+ 2) + (- 3) |$ ；
② $| - 2 | + | - 3 |$ $| (- 2) + (- 3) |$ ；
③ $| 0 | + | - 3 |$ $| 0 + (- 3) |$ ．

(2)、在（1）的基础上，嘉淇又举出若干个例子，并归纳得出以下结论，请你补充完整：
①当 $a$ ， $b$   ▲  （填“同号”或“异号” $)$ 时，有 $| a | + | b | > | a + b |$ ；
②当 $a$ ， $b$   ▲  （填“同号”或“异号” $)$ 时，有 $| a | + | b | = | a + b |$ ；
③当 $a$ ， $b$ 中至少有一个为0时，有 $| a | + | b |$   ▲   $| a + b |$ ．
总之，对于有理数 $a$ ， $b$ ，有 $| a | + | b |$   ▲   $| a + b |$ ．

(3)、根据上述结论，请你直接写出当 $| x | + 2023 = | x - 2023 |$ 时， $x$ 的取值范围．

查看试题解析

21. 某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入，下表是某周的生产情况(超产记为正、减产记为负)

星期	一	二	三	四	五	六	日
增减	+5	-2	-4	+12	-10	+16	-9

(1)、根据记录的数据可知该厂星期六生产自行车辆；

(2)、产量最多的一天比产量最少的一天多生产自行车辆；

(3)、根据记录的数据求出该厂本周实际生产自行车多少辆；

(4)、该厂实行每周计件工资制，每生产一辆车可得5050元，若超额完成任务，则超过部分每辆另奖1515元；少生产一辆扣2020元，那么该厂工人这一周的工资总额是多少元?

查看试题解析

2023年浙教版数学七年级上册2.1 有理数的加法 同步测试（培优版）

一、选择题

二、填空题

三、计算题

四、综合题

2023年浙教版数学七年级上册2.1 有理数的加法同步测试（培优版）