2023-2024学年苏科版数学九年级上册1.4用一元二次方程解决问题同步练习

试卷更新日期：2023-08-01 类型：同步测试

进入出卷网下载

一、选择题

1. 某校进行体操队列训练，原有8行10列，后增加40人，使得队伍增加的行数、列数相同，你知道增加了多少行或多少列吗？设增加了 $x$ 行或列，则列方程得（）

A、 (8﹣ ) (10﹣ )=8×10﹣40 B、 (8﹣ )(10﹣ )=8×10+40 C、 (8+ )(10+ )=8×10﹣40 D、 (8+ )(10+ )=8×10+40

查看试题解析
2.
王叔叔从市场上买了一块长80cm，宽70cm的矩形铁皮，准备制作一个工具箱．如图，他将矩形铁皮的四个角各剪掉一个边长xcm的正方形后，剩余的部分刚好能围成一个底面积为3000cm²的无盖长方形工具箱，根据题意列方程为（）

A、（80﹣x）（70﹣x）=3000 B、80×70﹣4x²=3000 C、（80﹣2x）（70﹣2x）=3000 D、80×70﹣4x²﹣（70+80）x=3000

查看试题解析
3. 如图，《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去高六尺，折高者几何？意思是：一根竹子，原高一丈（一丈＝十尺），一阵风将竹子折断，竹梢恰好抵地，抵地处离竹子底部6尺远，求折断处离地面的高度．设竹子折断处离地面x尺，根据题意，可列方程为（　　）

A、 $x^{2} + 6^{2} = 1 0^{2}$ B、 $（ 10 - x)^{2} + 6^{2} = x^{2}$ C、 $x^{2} + (10 - x)^{2} = 6^{2}$ D、 $x^{2} + 6^{2} = (10 - x)^{2}$

查看试题解析
4. 小明同学是一位古诗文的爱好者，在学习了一元二次方程这一章后，改编了苏轼诗词 $《$ 念奴娇 $\cdot$ 赤壁怀古 $》$ ：“大江东去浪淘尽，千古风流人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位平方与寿同．哪位学子算得快，多少年华数周瑜？”假设周瑜去世时年龄的十位数字是 $x$ ，则可列方程为（）

A、 $10 x + (x - 3) = (x - 3)^{2}$ B、 $10 (x + 3) + x = x^{2}$ C、 $10 x + (x + 3) = (x + 3)^{2}$ D、 $10 (x + 3) + x = (x + 3)^{2}$

查看试题解析
5. 在数学中，为了书写简便，18世纪数学家欧拉就引进了求和符号“ $\sum$ ”．如记 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + \cdot \cdot \cdot + (n - 1) + n$ ， $\sum_{k = 3}^{n} (x + k) = (x + 3) + (x + 4) + \cdot \cdot \cdot + (x + n)$ ；
已知 $\sum_{k = 2}^{n} [(x + k) (x - k + 1)] = 4 x^{2} + 4 x + m$ ，则m的值是（）

A、40 B、-70 C、-40 D、-20

查看试题解析
6. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有 $x$ 名同学，根据题意，列出方程为（）

A、 $x (x + 1) = 1035$ B、 $\frac{1}{2} x (x + 1) = 1035$ C、 $x (x - 1) = 1035$ D、 $\frac{1}{2} x (x - 1) = 1035$

查看试题解析
7. 某校九年级组织一次篮球赛，各班均组队参赛，每两班之间都进行两场比赛，共需比赛12场，则九年级班级的个数为（）

A、6 B、5 C、4 D、3

查看试题解析
8. 对于两个关于x的一元二次方程：F₁：ax²+bx+c＝0，F₂：cx²+bx+a＝0，其中a≠c．给出下列判断：
①若方程F₁有两个相等的实数根，则方程F₂也必有两个相等的实数根；
②若方程F₁有两个异号实根，则方程F₂也必有两个异号实根；
③若3是方程F₁的一个根，则 $\frac{1}{3}$ 必是方程F₂的一个根；
④若这两个方程有一个相同的根，则这个根必是1．
其中，正确的有（　　）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
9. 已知关于x的一元四次方程x⁴+px²+qx+r=0有三个相等的实根和另一个与之不同的实根，则下列三个命题中真命题有（　　）个

①p+q=r可能成立；②p+r=q可能成立；③q+r=p可能成立．

A、1 B、2 C、3 D、4

查看试题解析
10.
如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y= $\frac{1}{x}$ （x>0）的图像上，则点E的坐标为（）

A、( $\frac{1 + \sqrt{5}}{2}$ ， $\frac{\sqrt{5} - 1}{2}$ ) B、（1， $\frac{1}{2}$ ） C、（2， $\frac{1}{2}$ ） D、（ $\frac{\sqrt{2} + 1}{2}$ ， $\frac{\sqrt{2} - 1}{2}$ )

查看试题解析

二、填空题

11. 在学校劳动实践基地里有一块长20米、宽10米的长方形菜地，为了管理方便，准备沿平行于两边的方向纵、横开辟三条等宽的小道（如图中阴影部分所示），剩下部分种植蔬菜，已知种植蔬菜的面积为171平方米，则小道的宽为米．

查看试题解析
12. 方程x²-6x+8＝0的两个根是等腰三角形的底和腰，则这个等腰三角形周长是．

查看试题解析
13. 某校准备组织一次篮球比赛，参赛的每两个队之间都要比赛一场，赛程计划安排7天，每天安排4场比赛，那么共有个队参加.

查看试题解析
14. 有一个正方形的花园，如果它的边长增加 $2 m$ ，那么花园面积将增加 $16 m^{2}$ ，则原花园的面积为．

查看试题解析
15. 一次棋赛，有n个女选手和9n个男选手，每位参赛者与其 $10 n - 1$ 个选手各对局一次，计分方式为：胜者的2分，负者得0分，平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍，则n的所有可能值是.

查看试题解析

三、解答题

16. 如图1，荡秋千是中国古代北方少数民族创造的一种运动．有一天，小明在公园里游玩，如图2，他发现秋千静止时，踏板离地的垂直高度 $D E = 1 m$ ，将它往前推送 $6 m$ （水平距离 $B C = 6 m$ ）时，秋千的踏板离地的垂直高度 $B F = C E = 3 m$ ，秋千的绳索始终拉得很直，求绳索 $A D$ 的长度？

查看试题解析
17. 某中学读书社对全校600名学生图书阅读量（单位：本）进行了调查，第一季度全校学生人均阅读量是6本，读书社人均阅读量是15本．读书社人均阅读量在第二季度、第三季度保持一个相同的增长率x，全校学生人均阅读量第三季度和第一季度相比，增长率也是x，已知第三季度读书社全部40名成员的阅读总量将达到第三季度全校学生阅读总量的25%，求增长率x的值．

查看试题解析
18. 若两个连续整数的积是56，求这两个连续整数的和．

查看试题解析
19.
如图，某农场有一块长40m，宽32m的矩形种植地，为方便管理，准备沿平行于两边的方向纵、横各修建一条等宽的小路，要使种植面积为1140m² ，求小路的宽．

查看试题解析

四、综合题

20. 我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长各几何．（1丈＝10尺）
大意是：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．水的深度与这根芦苇的长度分别是多少？
将这个实际问题转化为数学问题，根据题意画出图形（如图所示），其中水面宽AB＝10尺，线段CD，CB表示芦苇，CD⊥AB于点E．

(1)、图中DE＝尺，EB＝尺；

(2)、求水的深度与这根芦苇的长度．

查看试题解析
21. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = a$ ， $A C = b (a < b)$ ， $A B = 5$ ， $a$ ， $b$ 是方程 $x^{2} - (m - 1) x + (m + 4) = 0$ 的两根.

(1)、求 $a$ ， $b$ ；

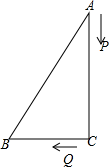(2)、 $P$ ， $Q$ 两点分别从 $A$ ， $C$ 出发，分别以每秒2个单位，1个单位的速度沿边 $A C$ ， $B C$ 向终点 $C$ ， $B$ 运动，（有一个点达到终点则停止运动），求经过多长时间后 $P Q = 2$ ？

查看试题解析
22.

(1)、【课本再现】要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场．根据场地和时间等条件，赛程计划安排7天，每天安排 $4$ 场比赛．
①共有场比赛；
②设比赛组织者应邀请 $x$ 个队参赛，每个队要与其他个队各赛一场，因为甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛，所以全部比赛场，列方程：．

(2)、【小试牛刀】
参加一次聚会的每两人都要握手一次，所有人共握手了10次，有多少人参加聚会？

(3)、【综合运用】
将 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， ……， $A_{n}$ ，共 $n$ 个点每两个点连一条线段共得到 $y_{1}$ 条线段，将 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， ……， $B_{2 n}$ ．共 $2 n$ 个点每两个点连一条线段共得到 $y_{2}$ 条线段，问 $\frac{y_{2}}{y_{1}}$ 能否为整数？写出你的结论，并说明理由．

查看试题解析
23. 已知 $x_{1}$ 、 $x_{2}$ 是关于x的一元二次方程 $x^{2} - 2 (n + 1) x + n^{2} + 5 = 0$ 的两实数根．

(1)、若 $(x_{1} - 1) (x_{2} - 1) = 28$ ，求n的值；

(2)、已知等腰三角形 $A B C$ 的一边长为7，若 $x_{1}$ 、 $x_{2}$ 恰好是△ $A B C$ 另外两边的长，求这个三角形的周长．

查看试题解析

2023-2024学年苏科版数学九年级上册1.4用一元二次方程解决问题 同步练习

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年苏科版数学九年级上册1.4用一元二次方程解决问题同步练习