2023-2024学年北师大版数学九年级上册6.3反比例函数的应用(提升卷)
试卷更新日期:2023-08-01 类型:同步测试
一、选择题
-
1. 如图,直线与x轴相交于点A , 与函数的图象交于点B,C,点B的横坐标是8,点C的横坐标是 , 则不等式组的解集是( )
 A、 B、 C、 D、2. 已知反比例函数(k为常数)的图象经过点 . 如图,过点B作直线 与函数的图象交于点A,与x轴交于点C,且 , 过点A作直线 , 交x轴于点F,则线段的长为( )
A、 B、 C、 D、2. 已知反比例函数(k为常数)的图象经过点 . 如图,过点B作直线 与函数的图象交于点A,与x轴交于点C,且 , 过点A作直线 , 交x轴于点F,则线段的长为( ) A、 B、 C、 D、3. 如图,直线y=kx-3(k≠0)与坐标轴分别交于点C,B,与双曲线y=-(x<0)交于点A(m,1),则AB的长是( )
A、 B、 C、 D、3. 如图,直线y=kx-3(k≠0)与坐标轴分别交于点C,B,与双曲线y=-(x<0)交于点A(m,1),则AB的长是( ) A、2 B、 C、2 D、4. 已知一次函数与反比例函数在同一平面直角坐标系中的图象如图所示,则当时,的取值范围是( )
A、2 B、 C、2 D、4. 已知一次函数与反比例函数在同一平面直角坐标系中的图象如图所示,则当时,的取值范围是( ) A、或 B、或 C、 D、5. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~4的整数),函数y=(x>0)的图象为曲线L.若曲线L使得T1~T4 , 这些点分布在它的两侧,每侧各2个点,则k的取值范围是( )
A、或 B、或 C、 D、5. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~4的整数),函数y=(x>0)的图象为曲线L.若曲线L使得T1~T4 , 这些点分布在它的两侧,每侧各2个点,则k的取值范围是( ) A、8≤k≤12 B、8≤k<12 C、8<k≤12 D、8<k<126. 如图,某加油站计划在地下修建一个容积为的圆柱形石油储存室,则储存室的底面积S(单位:)与其深度h(单位:m)的函数图象大致是( )
A、8≤k≤12 B、8≤k<12 C、8<k≤12 D、8<k<126. 如图,某加油站计划在地下修建一个容积为的圆柱形石油储存室,则储存室的底面积S(单位:)与其深度h(单位:m)的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,在平面直角坐标系中,在中,点在轴上, , 函数的图象经过点与边的中点 , 则的值为( )
7. 如图,在平面直角坐标系中,在中,点在轴上, , 函数的图象经过点与边的中点 , 则的值为( ) A、24 B、 C、36 D、8. 木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( )
A、24 B、 C、36 D、8. 木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( ) A、不大于1.5 m2 B、不小于1.5 m2 C、不大于m2 D、不小于m29. 如图,直线与x轴相交于点 , 与函数的图象交于点B、C,点B的横坐标是4,点C的横坐标是 , 则不等式组的解是( )
A、不大于1.5 m2 B、不小于1.5 m2 C、不大于m2 D、不小于m29. 如图,直线与x轴相交于点 , 与函数的图象交于点B、C,点B的横坐标是4,点C的横坐标是 , 则不等式组的解是( ) A、 B、 C、 D、10. 如图,等腰△ABC的顶点A在原点固定,且始终有AC=BC,当顶点C在函数y= (x>0)的图象上从上到下运动时,顶点B在x轴的正半轴上移动,则△ABC的面积大小变化情况是( )
A、 B、 C、 D、10. 如图,等腰△ABC的顶点A在原点固定,且始终有AC=BC,当顶点C在函数y= (x>0)的图象上从上到下运动时,顶点B在x轴的正半轴上移动,则△ABC的面积大小变化情况是( ) A、一直不变 B、先增大后减小 C、先减小后增大 D、先增大后不变
A、一直不变 B、先增大后减小 C、先减小后增大 D、先增大后不变二、填空题
-
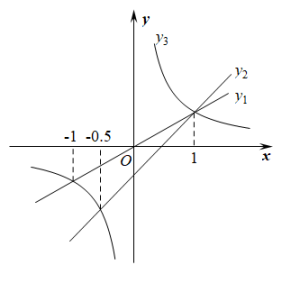
11. 如图,正比例函数 , 一次函数和反比例函数的图象在同一直角坐标系中,若 , 则自变量的取值范围是.
 12. 青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差小时.
12. 青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差小时. 13. 已知一次函数y=x-2的图象与反比例函数y=的图象相交于点P(a,b),则的值是 .14. 某工程队计划修建铁路,给出了铺轨的天数y(d)与每日铺轨量x(km/d)之间的关系表:
13. 已知一次函数y=x-2的图象与反比例函数y=的图象相交于点P(a,b),则的值是 .14. 某工程队计划修建铁路,给出了铺轨的天数y(d)与每日铺轨量x(km/d)之间的关系表:y(d)
120
150
200
240
300
x(km/d)
10
8
6
5
4
根据表格信息,判断出y是x的函数,则这个函数表达式是 .
15. 如图,正方形的边长为5,点A的坐标为 , 点B在y轴上,若反比例函数的图象过点C,则k的值为 .
三、综合题
-
16. 如图,点和是一次函数的图像与反比例函数的图像的两个交点.
 (1)、求m、n的值;(2)、求一次函数的表达式;(3)、设点P是y轴上的一个动点,当的周长最小时,求点P的坐标;(4)、在(3)的条件下,设点D是坐标平面内一个动点,当以点A、B、C、D为顶点的四边形是平行四边形时,请直接写出符合条件的所有点D的坐标.17. 《城镇污水处理厂污染物排放标准》中硫化物的排放标准为.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为;从第60小时开始,所排污水中硫化物的浓度是监测时间x(小时)的反比例函数,其图象如图所示.
(1)、求m、n的值;(2)、求一次函数的表达式;(3)、设点P是y轴上的一个动点,当的周长最小时,求点P的坐标;(4)、在(3)的条件下,设点D是坐标平面内一个动点,当以点A、B、C、D为顶点的四边形是平行四边形时,请直接写出符合条件的所有点D的坐标.17. 《城镇污水处理厂污染物排放标准》中硫化物的排放标准为.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为;从第60小时开始,所排污水中硫化物的浓度是监测时间x(小时)的反比例函数,其图象如图所示.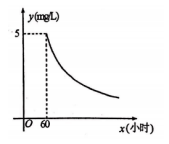 (1)、求y与x的函数关系式;(2)、整改开始第100小时时,所排污水中硫化物浓度为;(3)、按规定所排污水中硫化物的浓度不超过时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?18. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,其图象如下图所示所示.请根据图象中的信息解决下列问题:
(1)、求y与x的函数关系式;(2)、整改开始第100小时时,所排污水中硫化物浓度为;(3)、按规定所排污水中硫化物的浓度不超过时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?18. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米()的反比例函数,其图象如下图所示所示.请根据图象中的信息解决下列问题: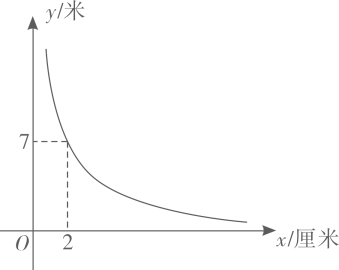 (1)、求y与x之间的函数表达式;(2)、当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为多少米?(3)、若某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是多少厘米?
(1)、求y与x之间的函数表达式;(2)、当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为多少米?(3)、若某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是多少厘米?

