2023-2024学年北师大版数学九年级上册6.2反比例函数的图象与性质(培优卷)
试卷更新日期:2023-08-01 类型:同步测试
一、选择题
-
1. 已知、、为双曲线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则2. 如图,的三个顶点的坐标分别为 , , , 将绕点顺时针旋转一定角度后使落在轴上,与此同时顶点恰好落在双曲线的图象上,则该反比例函数表达式为( )
 A、 B、 C、 D、3. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( )
A、 B、 C、 D、3. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( ) A、-8 B、-6 C、-4 D、-24. 如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( )
A、-8 B、-6 C、-4 D、-24. 如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( ) A、-2 B、-4 C、-6 D、-85. 如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B( , ),则k的值为( )
A、-2 B、-4 C、-6 D、-85. 如图,在平面直角坐标系中,菱形ABCO的顶点O在坐标原点,且与反比例函数y=的图象相交于A(m,3),C两点,已知点B( , ),则k的值为( ) A、-6 B、-6 C、-12 D、-126. 已知点A是双曲线y= 在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= (x>0)上运动,则k的值是( )
A、-6 B、-6 C、-12 D、-126. 已知点A是双曲线y= 在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= (x>0)上运动,则k的值是( )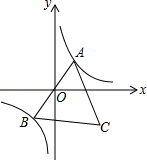 A、3 B、 C、﹣3 D、﹣7. 如图,点A是反比例图数y= (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
A、3 B、 C、﹣3 D、﹣7. 如图,点A是反比例图数y= (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )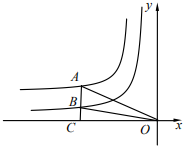 A、﹣4 B、﹣6 C、﹣8 D、﹣128. 如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上已知平行四边形ABCD的面积为6,则k的值为( )
A、﹣4 B、﹣6 C、﹣8 D、﹣128. 如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上已知平行四边形ABCD的面积为6,则k的值为( ) A、6 B、-6 C、3 D、-39. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
A、6 B、-6 C、3 D、-39. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( ) A、1<k<9 B、2≤k≤34 C、1≤k≤16 D、4≤k<1610. 如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).
A、1<k<9 B、2≤k≤34 C、1≤k≤16 D、4≤k<1610. 如图,在 轴正半轴上依次截取 ,过点 、 、 、…… 分别作 轴的垂线,与反比例函数 交于点 、 、 、…、 ,连接 、 、… ,过点 、 、…、 分别向 、 、…、 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).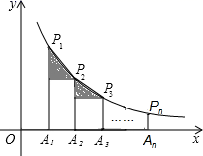 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知过原点的一条直线与反比例函数的图象交于 , 两点在的右侧.是反比例函数图象上位于点上方的一动点,连接并延长交轴于点 , 连接交轴于点.若 , 则.12. 如图,已知等边 , 顶点在双曲线上,点的坐标为 . 过作交双曲线于点 , 过作交轴于点 , 得到第二个等边;过作交双曲线于点 , 过作交轴于点 , 得到第三个等边;以此类推,…,则点的坐标为 .
 13. 如图,已知△P1OA1 , △P2A1A2 , △P3A2A3…△PnAn﹣1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数y=(x>0)的图象上,斜边OA1、A1A2、A2A3…An﹣1An都在x轴上.则点A2021的坐标为 .
13. 如图,已知△P1OA1 , △P2A1A2 , △P3A2A3…△PnAn﹣1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数y=(x>0)的图象上,斜边OA1、A1A2、A2A3…An﹣1An都在x轴上.则点A2021的坐标为 . 14. 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是.
14. 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是.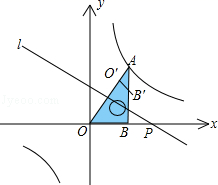 15. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn , 连接P1P2、P2P3、…、Pn﹣1Pn , 过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是
15. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn , 连接P1P2、P2P3、…、Pn﹣1Pn , 过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是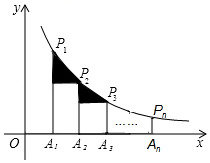
三、综合题
-
16. 如图1,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k>0)的第一象限内的图象上,OA=4,OC=3,动点P在y轴的右侧,且满足S△PCO=S矩形OABC.
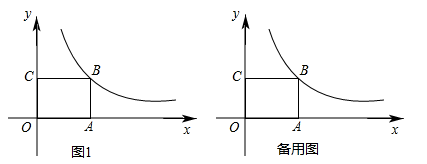 (1)、若点P在这个反比例函数的图象上,求点P的坐标;(2)、连接PO、PC,求PO+PC的最小值;(3)、若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.17. 如图,平行四边形OABC的边OA在x轴的正半轴上, , , CD平分∠OCB,CD交OA于点D,作DE⊥CD交AB于点E,反比例函数的图象经过点C与点E.
(1)、若点P在这个反比例函数的图象上,求点P的坐标;(2)、连接PO、PC,求PO+PC的最小值;(3)、若点Q是平面内一点,使得以B、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.17. 如图,平行四边形OABC的边OA在x轴的正半轴上, , , CD平分∠OCB,CD交OA于点D,作DE⊥CD交AB于点E,反比例函数的图象经过点C与点E. (1)、求k的值及直线CD的解析式;(2)、求证:;(3)、求点E的坐标.18. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整:
(1)、求k的值及直线CD的解析式;(2)、求证:;(3)、求点E的坐标.18. 已知一块矩形草坪的两边长分别是2米与3米,现在要把这个矩形按照如图1的方式扩大到面积为原来的2倍,设原矩形的一边加长a米,另一边长加长b米,可得a与b之间的函数关系式b=﹣2.某班“数学兴趣小组”对此函数进一步推广,得到更一般的函数y=﹣2,现对这个函数的图象和性质进行了探究,研究过程如下,请补充完整: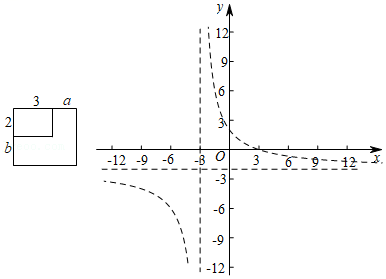 (1)、类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是 .(2)、“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;(3)、结合函数y=|﹣2|的图象解答下列问题:
(1)、类比反比例函数可知,函数y=﹣2的自变量x的取值范围是 , 这个函数值y的取值范围是 .(2)、“数学兴趣小组”进一步思考函数y=|﹣2|的图象和性质,请根据函数y=﹣2的图象,画出函数y=|﹣2|的图象;(3)、结合函数y=|﹣2|的图象解答下列问题:①求出方程|﹣2|=0的根;
②如果方程|﹣2|=a有2个实数根,请直接写出a的取值范围.
19. 已知点A(3,m+2),B(m+4,2)都在反比例函数y的图像上.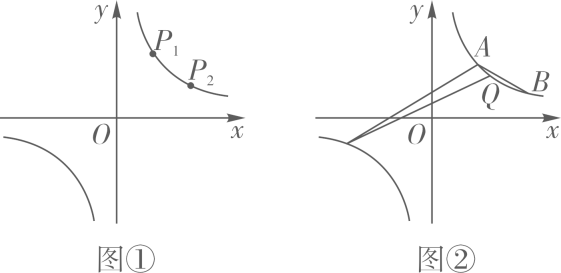 (1)、求m,k的值;(2)、如图①,已知反比例函数y的图像上有两点P1(x1 , y1),P2(x2 , y2),且0<x1<x2<3,分别过P1 , P2向x轴作垂线,垂足分别为M1 , M2 , 过P1 , P2向y轴作垂线,垂足分别为N1 , N2 . 若记四边形P1M1ON1和四边形P2M2ON2的周长分别为C1 , C2 , 试比较C1和C2的大小;并说明理由.(3)、如图②,若点B关于原点O对称点为C,点Q为双曲线AB段上任一动点,试探究∠ACQ与∠ABQ大小关系,并说明理由.20. 如图,四边形OABC为正方形,反比例函数的图象过AB上一点E,BE=2, .
(1)、求m,k的值;(2)、如图①,已知反比例函数y的图像上有两点P1(x1 , y1),P2(x2 , y2),且0<x1<x2<3,分别过P1 , P2向x轴作垂线,垂足分别为M1 , M2 , 过P1 , P2向y轴作垂线,垂足分别为N1 , N2 . 若记四边形P1M1ON1和四边形P2M2ON2的周长分别为C1 , C2 , 试比较C1和C2的大小;并说明理由.(3)、如图②,若点B关于原点O对称点为C,点Q为双曲线AB段上任一动点,试探究∠ACQ与∠ABQ大小关系,并说明理由.20. 如图,四边形OABC为正方形,反比例函数的图象过AB上一点E,BE=2, . (1)、求k的值.(2)、反比例函数的图象与线段BC交于点D,直线y=ax+b过点D及线段AB的中点F,探究直线OF与直线DF的位置关系,并证明.(3)、点P是直线OF上一点,当PD+PC的值最小时,求点P的坐标.
(1)、求k的值.(2)、反比例函数的图象与线段BC交于点D,直线y=ax+b过点D及线段AB的中点F,探究直线OF与直线DF的位置关系,并证明.(3)、点P是直线OF上一点,当PD+PC的值最小时,求点P的坐标.