2023-2024学年北师大版数学九年级上册6.1反比例函数（培优卷）

试卷更新日期：2023-08-01 类型：同步测试

进入出卷网下载

一、选择题

1. 若 $y = \frac{m (m - 3)}{x}$ 是反比例函数，则m满足的条件是（）

A、m≠0 B、m=3 C、m=3或m=0 D、m≠3且m≠0

查看试题解析
2. 已知反比例函数的解析式为 $y = \frac{| a | - 2}{x}$ ，则a的取值范围是 $($ 　　 $)$

A、 $a \neq 2$ B、 $a \neq - 2$ C、 $a \neq \pm 2$ D、 $a = \pm 2$

查看试题解析
3. 若面积为6cm²的平行四边形的一条边长为x(cm)，这条边上的高为y(cm)，则y关于x的函数表达式为（）

A、xy=12 B、xy=6 C、 $y = \frac{12}{x}$ D、 $y = \frac{6}{x}$

查看试题解析
4. 计划修建铁路 $l$ km，铺轨天数为 $t$ （d），每日铺轨量 $s$ （km/d），则在下列三个结论中，正确的是（）
①当 $l$ 一定时， $t$ 是 $s$ 的反比例函数；
②当 $l$ 一定时， $l$ 是 $s$ 的反比例函数；
③当 $s$ 一定时， $l$ 是 $t$ 的反比例函数．
A. B. C. D.

A、仅①． B、仅②． C、仅③． D、①，②，③．

查看试题解析
5. 已知用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P＝I²R，则下列说法中，正确的是（）

A、当P为定值时，I与R成反比例； B、当P为定值时，I²与R成反比例 C、当P为定值时，I与R成正比例； D、当P为定值时，I²与R成正比例

查看试题解析
6. 如果等腰三角形的底边长为x，底边上的高为y，它的面积为10时，则y与x的函数关系式为（）

A、 $y = \frac{10}{x}$ B、 $y = \frac{10}{2 x}$ C、 $y = \frac{20}{x}$ D、 $y = \frac{x}{20}$

查看试题解析
7. 已知水池的容量为50米³ ，每时灌水量为n米³ ，灌满水所需时间为t（时），那么t与n之间的函数关系式是（）

A、t=50n B、t=50﹣n C、t= $\frac{50}{n}$ D、t=50+n

查看试题解析
8. 下列问题情景中的两个变量成反比例的是（）

A、汽车沿一条公路从A地驶往B地所需的时间t与平均速度v B、圆的周长l与圆的半径r C、圆的面积s与圆的半径r D、在电阻不变的情况下，电流强度I与电压U

查看试题解析

二、填空题

9. 已知反比例函数 $y = (m - 1) x^{m^{2} - 2}$ ，则m= ，函数的表达式是.

查看试题解析
10. 当m=时，函数 $y = (m + 1) x^{m^{2} - 2}$ 是反比例函数．

查看试题解析
11. 某户家庭用购电卡购买了2 000度电，若此户家庭平均每天的用电量为x(单位：度)，这2 000度电能够使用的天数为y(单位：天)，则y与x的函数关系式为y＝.

查看试题解析
12. 一个物体重 100N，物体对地面的压强 P（单位：Pa）随物体与地面的接触面积 S（单位：㎡）变化而变化的函数关系式是.

查看试题解析
13. 验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据，如表：
y（单位：度）
100
200
400
500
…
x（单位：米）
1.00
0.50
0.25
0.20
…
则y关于x的函数关系式是．

查看试题解析

三、解答题

14. 给出下列四个关于是否成反比例的命题，判断它们的真假．

(1)、面积一定的等腰三角形的底边长和底边上的高成反比例；

(2)、面积一定的菱形的两条对角线长成反比例；

(3)、面积一定的矩形的两条对角线长成反比例；

(4)、面积一定的直角三角形的两直角边长成比例．

查看试题解析
15. 已知函数 $y = (k - 2) x^{k^{2} - k - 3}$ 是反比例函数，求 $k$ 的值.

查看试题解析
16. 已知函数 $y = (m - 1) x^{| m | - 2}$ 是反比例函数．

(1)、求m的值；

(2)、求当 $x = 3$ 时，y的值

查看试题解析
17. 已知一个长方体的体积是100cm³ ，它的长是ycm，宽是10cm，高是xcm．
（1）写出y与x之间的函数关系式；
（2）当x=2cm时，求y的值．

查看试题解析
18.
某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种，下图是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（小时）变化的函数图象，其中BC段是双曲线y= $\frac{k}{x}$ 的一部分．请根据图中信息解答下列问题：
（1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？
（2）求k的值；
（3）当x=18时，大棚内的温度约为多少度？

查看试题解析
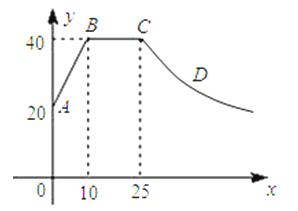
19.
心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？
（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

查看试题解析

y（单位：度）	100	200	400	500	…
x（单位：米）	1.00	0.50	0.25	0.20	…