2023-2024学年北师大版数学九年级上册5.1投影（提升卷）
试卷更新日期：2023-08-01 类型：同步测试
一、选择题
-
1. 如图所示，在房子的屋檐处安有一台监视器，房子前有一面落地的广告牌，那么监视器的盲区（ ）
A、△ACE B、△ADF C、△ABD D、四边形BCED2. 如图，在一间黑屋子的地面A处有一盏探照灯，当人从灯向墙运动时，他在墙上的影子的大小变化情况是（ ）
A、变大 B、变小 C、不变 D、不能确定3. 晚上，人在马路上走过一盏路灯的过程中，其影子长度的变化情况是（ ）A、先变短后变长 B、先变长后变短 C、逐渐变短 D、逐渐变长4. 如图，哪一个是太阳光下形成的影子？（ ）A、
B、
C、
D、
5. 如图，电灯在横杆的正上方，在灯光下的影长为 ， ， ， ， 点到的距离是 ， 则点到的距离是（ ）
A、 B、 C、 D、6. 太阳发出的光照在物体上是 ， 路灯发出的光照在物体上是 （ ）A、平行投影，中心投影 B、中心投影，平行投影 C、平行投影，平行投影 D、中心投影，中心投影7. 如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（ ）
A、12米 B、10.2米 C、10米 D、9.6米8. 如图，AB表示一个窗户的高，AM和BN表示射入室内的光线，窗户的下端到地面距离BC＝1米，已知某一时刻BC在地面的影长CN＝1.5米，AC在地面的影长CM＝4.5米，则AB高为（ ）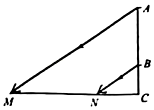
A、3.5 B、2 C、1.5 D、2.59. 如图，在直角坐标系中，点P(2，2)是一个光源．木杆AB两端的坐标分别为(0，1)，(3，1)．则木杆AB在x轴上的投影长为（ ）
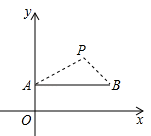A、3 B、4 C、5 D、610. 如图，在同一时刻，身高1.6米的小丽在阳光下的影长为2.5米，一棵大树的影长为5米，则这棵树的高度为（ ）
A、7.8米 B、3.2米 C、2.30米 D、1.5米二、填空题
-
11. 已知同一时刻物体的高与影子的长成正比例.身高的小明的影子长为 ， 这时测得一棵树的影长为 ， 则这棵树的高为.12. 如图，物体在灯泡发出的光照射下形成的影子是投影.（填“平行”或“中心”）.
13. 《孙子算经》是中国古代重要的数学著作，其中有首歌谣：“今有竿不知其长，量得影长一百五十寸，立一标杆，长一十五寸，影长五寸，问竿长几何？”．其意思是：“如图，有一根竹竿不知道有多长，量出它在太阳下的影子长150寸，同时立一根15寸的小标杆 ， 它的影子长5寸，则竹竿的长为多少？”．答：竹竿的长为寸．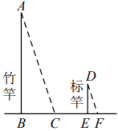
14. 在某一时刻，测得一根高为2m的竹竿的影长为1m，同时测得一栋建筑物的影长为13m，那么这栋建筑物的高度为m．15. 如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方，某一时刻，太阳光线恰好垂直照射叶片、 ， 此时各叶片影子在点M右侧成线段 ． 测得 ， ， 垂直于地面的木棒与影子的比为 ． 则点O、M之间的距离等于m；
三、综合题
-
16. 如图，郑明同学站在A处，测得他在路灯OC下影子AP的长与他的身高相等，都为1.5m，他向路灯方向走1m到B处时发现影子刚好落在A点.
(1)、请在图中画出形成影子的光线，并确定光源O的位置；(2)、求路灯OC的高.17. 如图，在路灯下，小明（用线段表示）的影子是 ， 在处有一棵大树（用线段表示），它的影子是 ．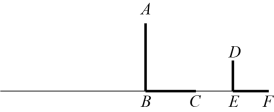
(1)、请确定路灯的位置（用点表示）；(2)、若身高1.6米的小明的影长3米，他在距离灯的底部18米处，求路灯的高度．18. 如图，一路灯与墙相距20米，当身高米的小亮在离墙17米的D处时，影长为1米．
(1)、求路灯B的高度；(2)、若点P为路灯，请画出小亮位于N处时，在路灯P下的影子NF（用粗线段表示出来）19. 【综合与实践】现实生活中，人们可以借助光源来测量物体的高度．已知榕树CD，FG和灯柱AB如图①所示，在灯柱AB上有一盏路灯P，榕树和灯柱的底端在同一水平线上，两棵榕树在路灯下都有影子，只要测量出其中一些数据，则可求出所需要的数据，具体操作步骤如下：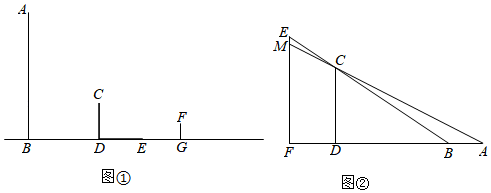
①根据光源确定榕树在地面上的影子；
②测量出相关数据，如高度，影长等；
③利用相似三角形的相关知识，可求出所需要的数据．
根据上述内容，解答下列问题：
(1)、已知榕树CD在路灯下的影子为DE，请画出榕树FG在路灯下的影子GH；(2)、如图①，若榕树CD的高度为3.6米，其离路灯的距离BD为6米，两棵榕树的影长DE，GH均为4米，两棵树之间的距离DG为6米，求榕树FG的高度；(3)、无论太阳光还是点光源，其本质与视线问题相同．日常生活中我们也可以直接利用视线解决问题．如图②，建筑物CD高为50米，建筑物MF上有一个广告牌EM，合计总高度EF为70米，两座建筑物之间的直线距离FD为30米．一个观测者（身高不计）先站在A处观测，发现能看见广告牌EM的底端M处，观测者沿着直线AF向前走了5米到B处观测，发现刚好看到广告牌EM的顶端E处．则广告牌EM的高度为 米．20. 小明想利用阳光下的影长测量学校旗杆 的高度.如图，他在某一时刻在地面上竖直立一个2米长的标杆 ，测得其影长 米.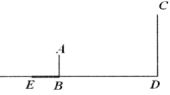
(1)、请在图中画出此时旗杆 在阳光下的投影 .(2)、如果 米，求旗杆 的高.