2023-2024学年北师大版数学九年级上册4.8图形的位似(基础卷)
试卷更新日期:2023-08-01 类型:同步测试
一、选择题
-
1. 如图,五边形与五边形是位似图形,O为位似中心, , 则为( )
 A、2:3 B、3:2 C、1:2 D、2:12. 在如图所示的人眼成像的示意图中,可能没有蕴含的初中数学知识是( )
A、2:3 B、3:2 C、1:2 D、2:12. 在如图所示的人眼成像的示意图中,可能没有蕴含的初中数学知识是( ) A、位似图形 B、相似三角形的判定 C、旋转 D、平行线的性质3. 如图,在平面直角坐标系中,将 OAB以原点O为位似中心放大后得到 OCD,若B(0,1),D(0,3),则 OAB与 OCD的面积比是( )
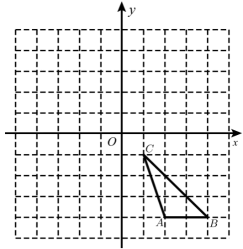
A、位似图形 B、相似三角形的判定 C、旋转 D、平行线的性质3. 如图,在平面直角坐标系中,将 OAB以原点O为位似中心放大后得到 OCD,若B(0,1),D(0,3),则 OAB与 OCD的面积比是( ) A、2:1 B、1:3 C、1:9 D、9:14. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,位似比为1:2,设点B的横坐标是a,则点B的对应点B′的横坐标是( ).
A、2:1 B、1:3 C、1:9 D、9:14. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,位似比为1:2,设点B的横坐标是a,则点B的对应点B′的横坐标是( ).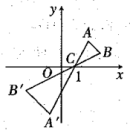 A、 B、 C、 D、5. 如图,线段两个端点的坐标分别为 , , 以原点为位似中心,在第一象限内将线段缩小为原来的后得到线段 , 则点的坐标为( )
A、 B、 C、 D、5. 如图,线段两个端点的坐标分别为 , , 以原点为位似中心,在第一象限内将线段缩小为原来的后得到线段 , 则点的坐标为( ) A、 B、 C、 D、6. 如图,以O为位似中心且与ABC位似的图形编号是( )
A、 B、 C、 D、6. 如图,以O为位似中心且与ABC位似的图形编号是( )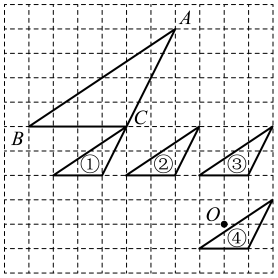 A、① B、② C、③ D、④7. 在平面直角坐标系中,点A(6,3),以原点O为位似中心,在第一象限内把线段OA缩小为原来的 得到线段OC,则点C的坐标为( )A、(2,1) B、(-2,-1) C、(2,2) D、(2,1)或(-2,-1)8. 如图,在△AOB中,A,B两点在x轴上方,以点O为位似中心,在x轴的下方作△AOB的位似图形△ ,把△AOB的边长放大到原来的2倍,设点B的对应点 的坐标是(4,﹣2),则点B的坐标是( )
A、① B、② C、③ D、④7. 在平面直角坐标系中,点A(6,3),以原点O为位似中心,在第一象限内把线段OA缩小为原来的 得到线段OC,则点C的坐标为( )A、(2,1) B、(-2,-1) C、(2,2) D、(2,1)或(-2,-1)8. 如图,在△AOB中,A,B两点在x轴上方,以点O为位似中心,在x轴的下方作△AOB的位似图形△ ,把△AOB的边长放大到原来的2倍,设点B的对应点 的坐标是(4,﹣2),则点B的坐标是( ) A、(2,1) B、(2,﹣1) C、(﹣2,1) D、(﹣2,﹣1)9. 在平面直角坐标系中,线段 两个端点的坐标分别为 .若以原点 为位似中心,在第三象限内将线段 扩大为原来的2倍得到线段 ,则点 的对应点 的坐标为( )A、 B、 C、 D、10. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,以下说法错误的是( )
A、(2,1) B、(2,﹣1) C、(﹣2,1) D、(﹣2,﹣1)9. 在平面直角坐标系中,线段 两个端点的坐标分别为 .若以原点 为位似中心,在第三象限内将线段 扩大为原来的2倍得到线段 ,则点 的对应点 的坐标为( )A、 B、 C、 D、10. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,以下说法错误的是( ) A、点A,O, 三点在同一条直线上 B、 C、 D、
A、点A,O, 三点在同一条直线上 B、 C、 D、二、填空题
-
11. 如图,以点为位似中心,将五边形放大后得到五边形 , 已知 , , 五边形的周长为 , 则五边形的周长是.
 12. 如图,△OAB与△OCD是以点O为位似中心的位似图形,位似比为1:2,∠OCD=90°,CO=CD=2,则点B的坐标为 .
12. 如图,△OAB与△OCD是以点O为位似中心的位似图形,位似比为1:2,∠OCD=90°,CO=CD=2,则点B的坐标为 . 13. 在平面直角坐标系中,已知点A(2,1),B(6,4),以原点O为位似中心,在第一象限内把△AOB按相似比1:2缩小,则点B的对应点B′的坐标是.14. 如图, 三个顶点的坐标分别为 ,以原点O为位似中心,把这个三角形缩小为原来的 ,可以得到 ,已知点 的坐标是 ,则点 的坐标是.
13. 在平面直角坐标系中,已知点A(2,1),B(6,4),以原点O为位似中心,在第一象限内把△AOB按相似比1:2缩小,则点B的对应点B′的坐标是.14. 如图, 三个顶点的坐标分别为 ,以原点O为位似中心,把这个三角形缩小为原来的 ,可以得到 ,已知点 的坐标是 ,则点 的坐标是.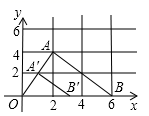 15. 如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为.
15. 如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为.
三、作图题
-
16. 如图,由若干个边长为1的小正方形组成的网格中,已知格点线段 (端点是网格线的交点)和格点 .
 (1)、以点 为位似中心,画出线段 的位似图形线段 ,使线段 与线段 的相似比为2;(2)、以点 为旋转中心,画出线段 绕点 顺时针旋转90°得到的线段 .17. 如图, 的顶点都在方格线的交点(格点)上,按下列要求作答.
(1)、以点 为位似中心,画出线段 的位似图形线段 ,使线段 与线段 的相似比为2;(2)、以点 为旋转中心,画出线段 绕点 顺时针旋转90°得到的线段 .17. 如图, 的顶点都在方格线的交点(格点)上,按下列要求作答. (1)、以原点O为位似中心,将 放大为原来的 倍,得到 ,请在所给的坐标系中作出一个满足条件的图形;(2)、写出你所画图形中 , , 点的坐标.
(1)、以原点O为位似中心,将 放大为原来的 倍,得到 ,请在所给的坐标系中作出一个满足条件的图形;(2)、写出你所画图形中 , , 点的坐标.四、综合题
-
18. 方格图中的每个小方格都是边长为1小正方形,我们把小正方形的顶点称为格点,格点连线为边的四边形称为“格点四边形”,图1中的四边形ABCD就是一个格点四边形.
 (1)、小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答:四边形ABCD与四边形EFGH相似吗?若相似,直接写出四边形ABCD与四边形EFGH的相似比;若不相似说明理由;(2)、请在图3的方格图中画一个格点四边形,使它与四边形ABCD相似,但与四边形ABCD、四边形EFGH都不全等.
(1)、小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答:四边形ABCD与四边形EFGH相似吗?若相似,直接写出四边形ABCD与四边形EFGH的相似比;若不相似说明理由;(2)、请在图3的方格图中画一个格点四边形,使它与四边形ABCD相似,但与四边形ABCD、四边形EFGH都不全等.