2023年浙教版数学九年级上册3.2 图形的旋转 同步测试(提高版)
试卷更新日期:2023-08-01 类型:同步测试
一、选择题
-
1. 如图,将含有锐角的三角板绕的锐角顶点C逆时针旋转到 , 、相交于点F,连接 , 若 , 则旋转角的度数为( )
 A、 B、 C、 D、2. 如图,在△ABC中,∠BAC=90°,AB=6,AC=8.将△ABC绕点A旋转至△ADE,使AD⊥BC,DE交边AC于点F,则AF的长是( )
A、 B、 C、 D、2. 如图,在△ABC中,∠BAC=90°,AB=6,AC=8.将△ABC绕点A旋转至△ADE,使AD⊥BC,DE交边AC于点F,则AF的长是( ) A、4 B、 C、5 D、63. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在边AB上,则点与点B之间的距离为( )
A、4 B、 C、5 D、63. 如图,在Rt△ABC中, , , , 将△ABC绕点C按逆时针方向旋转得到 , 此时点恰好在边AB上,则点与点B之间的距离为( ) A、4 B、2 C、3 D、4. 如图,将绕点逆时针旋转,得到 , 若点A的对应点恰好在线段上,且平分 , 记线段与线段的交点为 . 下列结论中,错误的是( )
A、4 B、2 C、3 D、4. 如图,将绕点逆时针旋转,得到 , 若点A的对应点恰好在线段上,且平分 , 记线段与线段的交点为 . 下列结论中,错误的是( )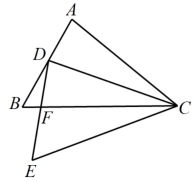 A、 B、 C、 D、5. 如图,将线段AB绕点O顺时针旋转90°得到线段 , 那么的对应点的坐标是( )
A、 B、 C、 D、5. 如图,将线段AB绕点O顺时针旋转90°得到线段 , 那么的对应点的坐标是( ) A、 B、 C、 D、6. 如图,在等腰中, , 将绕点逆时针旋转得到 , 当点的对应点落在上时,连接 , 则的度数是( )
A、 B、 C、 D、6. 如图,在等腰中, , 将绕点逆时针旋转得到 , 当点的对应点落在上时,连接 , 则的度数是( )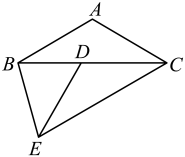 A、30° B、45° C、55° D、75°7. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
A、30° B、45° C、55° D、75°7. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )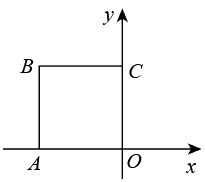 A、 B、 C、 D、8. 如图,中,已知 , , 点D在边上,线段绕着点逆时针旋转()后,如果点A恰好落在边上,那么的度数是( )
A、 B、 C、 D、8. 如图,中,已知 , , 点D在边上,线段绕着点逆时针旋转()后,如果点A恰好落在边上,那么的度数是( ) A、50° B、60° C、80° D、120°9. 如图,在正方形ABCD中,AB=4,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( )
A、50° B、60° C、80° D、120°9. 如图,在正方形ABCD中,AB=4,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( ) A、3 B、2 C、5 D、10. 如图,在矩形中,是对角线,将矩形绕点顺时针旋转到位置,是的中点,若 , , 则线段的长为( )
A、3 B、2 C、5 D、10. 如图,在矩形中,是对角线,将矩形绕点顺时针旋转到位置,是的中点,若 , , 则线段的长为( ) A、 B、6 C、5 D、
A、 B、6 C、5 D、二、填空题
-
11. 如图,在△BDE中,∠BDE=90°, BD=4,点D的坐标是( 6,0) ,∠BDO=15°,将 BDE 旋转到 △ABC的位置,点C 在 BD上,则旋转中心的坐标为 .
 12. 如图,在中, , 将绕点逆时针旋转得到 , 若点恰好为的中点,则的长为 (用含的代数式表示).
12. 如图,在中, , 将绕点逆时针旋转得到 , 若点恰好为的中点,则的长为 (用含的代数式表示). 13. 如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1 , 当C1D1第一次经过顶点C时,旋转角∠ABA1= .
13. 如图,在平行四边形ABCD中,∠A=75°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1 , 当C1D1第一次经过顶点C时,旋转角∠ABA1= .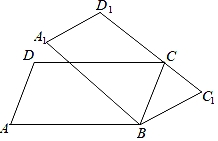 14. 如图,在直角三角形中, , , 将顺时针旋转得到 , 与相交于点 , 则的长为 . (结果保留根号)
14. 如图,在直角三角形中, , , 将顺时针旋转得到 , 与相交于点 , 则的长为 . (结果保留根号) 15. 将△OAB按如图的方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(1,),将△OAB绕原点O逆时针旋转60°得到点△OA'B′,则点A'的坐标为.
15. 将△OAB按如图的方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(1,),将△OAB绕原点O逆时针旋转60°得到点△OA'B′,则点A'的坐标为. 16. 如图,点A、B、C、D、O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为 .
16. 如图,点A、B、C、D、O都在方格纸上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为 .
三、作图题
-
17. 如图,的三个顶点都在边长为1的小正方形组成的网格的格点上,以点为原点建立直角坐标系,回答下列问题:

⑴将先向上平移5个单位,再向右平移1个单位得到 , 画出 , 并直接写出的坐标 ▲ ;
⑵将绕点顺时针旋转90°得到 , 画出;
⑶观察图形发现,是由绕点 ▲ (写出点的坐标)顺时针旋转 ▲ 度得到的.
四、综合题
-
18. 如图,将△ABC绕点A顺时针旋转得到△AED,并使C点的对应点D点落在直线BC上,
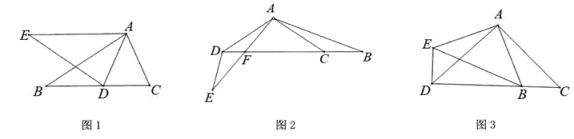 (1)、如图1,证明:DA平分∠EDC;(2)、如图2,AE与BD交于点F,若∠AFB=50°,∠B=20°,求∠BAC的度数;(3)、如图3,连接BE,若EB=13,ED=5,CD=17,则AD的长为 .19. 如图, 线段 两端点坐标分别为 .
(1)、如图1,证明:DA平分∠EDC;(2)、如图2,AE与BD交于点F,若∠AFB=50°,∠B=20°,求∠BAC的度数;(3)、如图3,连接BE,若EB=13,ED=5,CD=17,则AD的长为 .19. 如图, 线段 两端点坐标分别为 .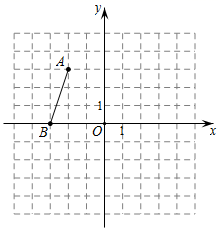 (1)、作出线段 绕点 逆时针旋转 后得到的线段 ;(2)、点 的坐标为 ,若线段 上有一点 , 则在线段 上的对应点 的 坐标为.(3)、若将线段 绕着某点旋转 恰好得到线段 , 点 与点 , 点 与点 是对应点,已知点 . 请通过无刻度的直尺画图找到旋转中心,将其标记为 .(保留作图痕迹)20. 如图,抛物线y= ax2﹣ax﹣4交x轴于点A,C,交y轴于点B,AC=6.
(1)、作出线段 绕点 逆时针旋转 后得到的线段 ;(2)、点 的坐标为 ,若线段 上有一点 , 则在线段 上的对应点 的 坐标为.(3)、若将线段 绕着某点旋转 恰好得到线段 , 点 与点 , 点 与点 是对应点,已知点 . 请通过无刻度的直尺画图找到旋转中心,将其标记为 .(保留作图痕迹)20. 如图,抛物线y= ax2﹣ax﹣4交x轴于点A,C,交y轴于点B,AC=6. (1)、求抛物线的解析式;(2)、点P为x轴上一动点,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点P的坐标.21. 在△ABC中,AB=AC,点D为平面内一点.
(1)、求抛物线的解析式;(2)、点P为x轴上一动点,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点P的坐标.21. 在△ABC中,AB=AC,点D为平面内一点. (1)、观察猜想:如图1,当∠BAC=90°,点D在BC上时,探究BD2、DC2与AD2之间的数量关系,我们可以把△ABD绕着点A逆时针旋转90°得△ACE,根据图形,请你通过探究直接写出BD2、DC2与AD2之间的数量关系:;(2)、类比探究:如图2,当∠BAC=60°时,点D为△ABC外一点,将△ABD顺时针旋转后得到△BCE若D、E、C三点在一直线上,求∠ADB的度数;(3)、拓展应用:如图3,已知∠BAC=∠BDA=120°,DC=10,AD=2 , 求BD的长.22. 如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.
(1)、观察猜想:如图1,当∠BAC=90°,点D在BC上时,探究BD2、DC2与AD2之间的数量关系,我们可以把△ABD绕着点A逆时针旋转90°得△ACE,根据图形,请你通过探究直接写出BD2、DC2与AD2之间的数量关系:;(2)、类比探究:如图2,当∠BAC=60°时,点D为△ABC外一点,将△ABD顺时针旋转后得到△BCE若D、E、C三点在一直线上,求∠ADB的度数;(3)、拓展应用:如图3,已知∠BAC=∠BDA=120°,DC=10,AD=2 , 求BD的长.22. 如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.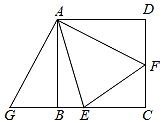 (1)、求证:GE=FE;(2)、若DF=3,求BE的长.
(1)、求证:GE=FE;(2)、若DF=3,求BE的长.
-

