2023-2024学年北师大版数学九年级上册3.1用树状图或表格求概率（培优卷）

试卷更新日期：2023-07-31 类型：同步测试

进入出卷网下载

一、选择题

1. 某校九年级学生中有5人在省数学竞赛中获奖，其中3人获一等奖，2人获二等奖．老师从5人中选2人向全校学生介绍学好数学的经验，则选出的2人中恰好一人是一等奖获得者，一人是二等奖获得者的概率是（）．

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
2. 有三张卡片，正面分别写有 $A$ 、 $B$ 、 $C$ 三个字母，其它完全相同，反扣在桌面上混合均匀，从中在取两张，同时取到 $A$ 、 $B$ 的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{2}{9}$

查看试题解析
3. 有五张卡片的正面分别写有“喜”“迎”“二”“十”“大”，五张卡片洗匀后将其反面朝上放在桌面上，小明从中任意抽取两张卡片，恰好是“二十”的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{20}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
4. 在今年“十一”期间，小康和小明两家准备从华山、华阳古镇，太白山三个著名景点中分别选择一个景点旅游，他们两家去同一景点旅游的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
5. 有两组卡片，第一组卡片上写有a，b，b，第二组卡片上写有a，b，b，c，c，求从每组卡片中各抽出一张，都抽到b的概率是（）

A、 $\frac{4}{15}$ B、 $\frac{8}{15}$ C、 $\frac{1}{2}$ D、 $\frac{4}{9}$

查看试题解析
6. 有4张背面相同的卡片，正面分别印有平行四边形、矩形、菱形、正方形，现将4张卡片正面朝下一字摆开，从中随机抽取两张，抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
7. 有2名男生和2名女生，王老师要随机地、两两一对地为他们排座位，一男一女排在一起的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. 为了深化落实“双减”工作，促进中小学生健康成长，教育部门加大了实地督查的力度，对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查，计划从“五项管理”中随机抽取两项进行问卷调查，则抽到“作业”和“手机”的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{5}$ C、 $\frac{1}{10}$ D、 $\frac{2}{25}$

查看试题解析
9. 经过某十字路口的汽车，可能直行，也可能向左转或向右转．如果这三种可能性大小相同，甲、乙两辆汽车经过这个十字路口时，一辆车向左转，一辆车向右转的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{2}{9}$ D、 $\frac{4}{9}$

查看试题解析
10. 有三条带子，第一条的一头是黑色，另一头是黄色，第二条的一头是黄色，另一头是白色，第三条的一头是白色，另一头是黑色．若任意选取这三条带子的一头，颜色各不相同的概率是（）．

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析

二、填空题

11. 把只有颜色不同的1个白球和2个红球装入一个不透明的口袋里搅匀，从中随机地摸出1个球后放回搅匀，再次随机地摸出1个球，两次都摸到红球的概率为

查看试题解析
12. 育才学校积极开展志愿者服务活动，来自初三的3名同学（1男2女）组成了“关爱老人”志愿小分队．若从该小分队中任选2名同学参加周末的志愿活动，则恰好是1男1女的概率是．

查看试题解析
13. 如图：麻将是中国的国粹之一，玩法最为复杂有趣，是中国古人发明的一种博弈游戏．它开局拿牌要投两枚骰子，将两枚骰子的点数相加之和除以4看余数来决定是在哪家开始拿牌．余数为1则在自家拿牌，余数为2就在下家拿牌，余数为3则在对家拿牌，能被4整除就在上家拿牌，则在自家拿牌的概率为．

查看试题解析
14. 如图，甲乙两人在玩转盘游戏时，把转盘A、B分成4等份、3等份，并在每一份内标上数字，并规定游戏规则如下：转动两个转盘各一次，转盘停止后，若指针所指的两个数字之和不大于8，则甲获胜，否则是乙获胜，则甲获胜的概率是．

查看试题解析
15. “双减”政策后，各校积极探索“课内提质增效，课后丰富多彩”的有效策略，某校的课后服务活动设置了四大板块课程： $A$ ．体育活动； $B$ 劳动技能； $C$ 经典阅读； $D$ 科普活动．若小明和小亮两人随机选择一个板块课程，则两人所选的板块课程恰好相同的概率是．

查看试题解析

三、综合题

16. 有甲乙两个不透明的布袋，甲布袋装有2个形状和重量完全相同的小球，分别标有数字1和2；乙布袋装有3个形状和重量完全相同的小球，分别标有数字﹣3，﹣1和0．先从甲布袋中随机取出一个小球，将小球上标有的数字记作x；再从乙布袋中随机取出一个小球，再将小球标有的数字记作y．

(1)、用画树状图或列表法写出两次摸球的数字可能出现的所有结果；

(2)、若从甲、乙两布袋中取出的小球上面的数记作点的坐标（x，y），求点（x，y）在一次函数y=﹣2x+1图象上的概率是多少？

查看试题解析
17. 为规范学生的在校表现，某班实行了操行评分制，根据学生的操行分高低分为A、B、C、D四个等级．现对该班上学期的操行等级进行了统计，并绘制了不完整的两种统计图，请根据图象回答问题：

(1)、该班的总人数为人，得到等级A的学生人数在扇形统计图中的圆心角度数是；

(2)、补全条形统计图；

(3)、已知男生小伟和女生小颖的操行等级都是A，且获得等级A的学生中有2名男生，现班主任打算从操行等级为A的男生和女生中各任意抽取一名作为代表，参加学校的年度表彰大会，请用树状图或列表法求出抽到的代表中有小伟或小颖的概率．

查看试题解析
18. 图①是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字1，2，3，4，图②是一个正六边形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子掷出后，看骰子向上三个面（除底面外）的数字之和是几，就从图②中的A点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法跳动．

(1)、随机掷一次骰子，则棋子跳动到点C处的概率是

(2)、随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点C处的概率．

查看试题解析
19.
某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：

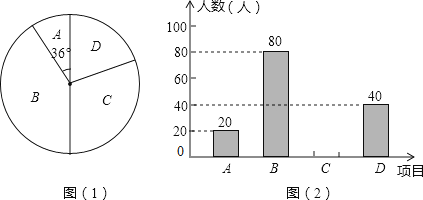(1)、这次被调查的学生共有人；

(2)、请你将条形统计图（2）补充完整；

(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率.（用树状图或列表法解答）

查看试题解析
20. 有A、B、C三把锁，其中A锁配了一把钥匙a，B锁配了一把钥匙b，C锁配了一把钥匙c，对于每把锁，只有用所配的钥匙才能打开，请根据题意，解决下列问题．

(1)、从三把钥匙中，随机选取一把，求所选钥匙恰好能打开C锁的概率．

(2)、从三把锁和三把钥匙中，随机选取两边锁和两把钥匙，若用选取的钥匙开选取的锁，求只能打开一把锁的概率．

查看试题解析