2023-2024学年北师大版数学九年级上册4.7相似三角形的性质（培优卷）

试卷更新日期：2023-07-31 类型：同步测试

进入出卷网下载

一、选择题

1. 如图是一个由A、B、C三种相似的直角三角形纸片拼成的矩形，A、B、C的纸片的面积分别为S₁、S₂、S₃ ，（S₁与S₂ ， S₂与S₃的相似比相同），相邻纸片之间互不重叠也无缝隙，若S₁＞S₂＞S₃ ，则这个矩形的面积一定可以表示为（）

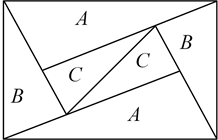A、4S₁ B、6S₂ C、4S₂+3S₃ D、3S₁+4S₃

查看试题解析
2. 如图，已知直角坐标系中四点A（﹣2，4）、B（﹣2，0）、C（2，﹣3）、D（2，0）.若点P在x轴上，且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似，则所有符合上述条件的点P的个数是（　　）

A、1个 B、2个 C、3 个 D、4个

查看试题解析
3. 如图，将Rt△ABC平移到△A′B′C′的位置，其中∠C＝90°，使得点C′与△ABC的内心重合，已知AC＝4，BC＝3，则阴影部分的周长为（）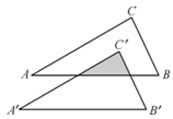

A、5 B、6 C、7 D、8

查看试题解析
4. 如图，点D是△ABC的边AC的上一点，且∠ABD=∠C；如果 $\frac{A D}{C D} = \frac{1}{3}$ ，那么 $\frac{B D}{B C}$ =（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
5. 已知 $△ A B C ∽ △ D E F ， S_{△ A B C} ： S_{△ D E F} = 1 ： 4$ ．则它们的周长比为（）

A、 $1 ： 2$ B、 $1 ： 4$ C、 $2 ： 1$ D、 $4 ： 1$

查看试题解析
6. 已知 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ ， $A D$ 和 $A^{'} D^{'}$ 是它们的对应高线，若 $A D = 4$ ， $A^{'} D^{'} = 2$ ，则 $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 的周长比是（）

A、2：1 B、2：3 C、4：1 D、4：9

查看试题解析
7. 已知 $△$ ABC∽ $△$ A₁B₁C₁ ，且 $\frac{A B}{A_{1} B_{1}}$ ＝ $\frac{2}{3}$ ．若 $△$ ABC的面积为4，则 $△$ A₁B₁C₁的面积是（）

A、 $\frac{8}{3}$ B、6 C、9 D、18

查看试题解析
8. 已知一个三角形的三边长分别为2，3，4，与其相似的另一个三角形的周长为36，则它的最长边的长为（）

A、8 B、12 C、16 D、20

查看试题解析
9. 如图，在 $10 \times 6$ 的方格纸中，每个小方格都是边长为1的正方形，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形.点E是格点四边形ABCD的AB边上一动点，连接ED，EC，若格点 $△ D A E$ 与 $△ E B C$ 相似，则 $D E + E C$ 的长为（）

A、 $3 \sqrt{13}$ B、 $\sqrt{149}$ C、 $3 \sqrt{13}$ 或 $5 \sqrt{5}$ D、 $3 \sqrt{13}$ 或 $\sqrt{149}$

查看试题解析
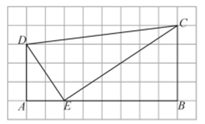10. 如果两个相似三角形的对应边之比为2：5，其中一个三角形的一个内角的角平分线长为7，则另一个三角形对应角平分线的长为（）

A、 $\frac{35}{2}$ B、 $\frac{14}{5}$ C、 $\frac{35}{2}$ 或 $\frac{14}{5}$ D、无法确定

查看试题解析

二、填空题

11. 如图， $△ A B C ∽ △ C B D$ ， $A B = 4$ ， $B D = 6$ ，则 $B C =$ .

查看试题解析
12. 若△ABC∽△A′B′C′，且 $\frac{A B}{A^{'} B^{'}} = \frac{3}{4}$ ， △ABC的周长为12cm，则△A′B′C′的周长为.

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以顶点 $A$ 为圆心，适当长为半径画弧，分别交 $A B$ ， $A C$ 于点 $N$ ， $M$ ，再分别以点 $M N$ 为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点 $P$ ，射线交边 $C$ 于点 $D$ ，若 $△ D A C ∽ △ A B C$ ，则 $∠ B =$ 度．

查看试题解析
14. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ，在 $B C$ 的延长线上截取 $B D = A B$ ，连接 $A D$ ，过点 $B$ 作 $B E ⊥ A D$ 于点 $E$ ，交 $A C$ 于点 $F$ ，连接 $D F$ ，点 $P$ 为射线 $B E$ 上一个动点，若 $A C = 9$ ， $B C = 12$ ，当 $△ A P B$ 与 $△ A F D$ 相似时， $B P$ 的长为．

查看试题解析
15. 如图，在直角梯形ABCD中， $A D ∥ B C$ ， $∠ D A B = 90 °$ ， $A B = 14$ ， $A D = 4$ ， $B C = 6$ ，动点P从点A出发，以每秒2个单位的速度向点B运动，运动到B点停止，若以点P，A，D为顶点的三角形与 $△ P B C$ 相似时，运动时间 $t =$ ．

查看试题解析

三、解答题

16. 如图，在 $△ A B C$ 中， $A B = 8 c m$ ， $B C = 16 c m$ ，点 $P$ 从点 $A$ 出发沿 $A B$ 边想向点 $B$ 以 $2 c m / s$ 的速度移动，点 $Q$ 从点 $B$ 出发沿 $B C$ 边向点 $C$ 以 $4 c m / s$ 的速度移动，如果 $P$ 、 $Q$ 同时出发，经过几秒后 $△ P B Q$ 和 $△ A B C$ 相似？

查看试题解析
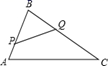17. 如图，在△ABC中，AB=4cm，BC=8cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，如果P、Q分别从A、B同时出发，经几秒后，点P、B、Q构成的三角形△PBQ与△ABC相似?

查看试题解析
18. 已知在△ABC中，∠ABC=90°，AB=3cm，BC=4cm．动点Q从点A出发沿AC向终点C匀速运动，速度2cm/s；同时，点P从点B出发沿BA向终点A匀速运动，速度1cm/s；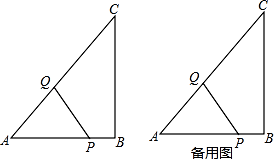

(1)、当t为何值时，△APQ与△ABC相似？

(2)、当t为何值时，△APQ为等腰三角形？

查看试题解析
19. 如图，已知在四边形ABCD中，AD∥BC，∠A＝90°，AB＝7，AD＝2，BC＝3.在线段AB上是否存在一点P，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似？若不存在，请说明理由；若存在，这样的点P有几个？

查看试题解析
20. 如图，在△ABC中，AB＝8cm，BC＝16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q从点B开始沿BC向C点以4cm/s的速度移动，如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？

查看试题解析