江西省萍乡市2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-31 类型:期末考试
一、单选题
-
1. 下列式子是分式的是( )A、 B、 C、 D、2. 在数轴上到原点的距离小于2的点所表示的数满足( )A、 B、或 C、 D、3. 在中,和的度数如下,能判定是等腰三角形的是( )A、 , B、 , C、 , D、 ,4. 下列因式分解正确的是( )A、 B、 C、 D、5. 如图,将绕点逆时针旋转得到 , 点和点是对应点,若 , , 则的长为( )
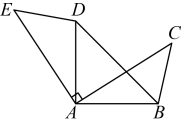 A、2 B、 C、4 D、6. 若关于的不等式组:无解,则的取值范围是( )A、 B、 C、 D、7. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
A、2 B、 C、4 D、6. 若关于的不等式组:无解,则的取值范围是( )A、 B、 C、 D、7. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )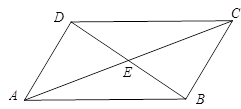 A、6 B、12 C、20 D、248. 若关于 的分式方程 的解为正数,则满足条件的正整数 的值为( )A、 B、 C、 D、9. 如图,在中, , 为内一点,过点的直线分别交、于点 , , 若在的垂直平分线上,在的垂直平分线上,则的度数为( )
A、6 B、12 C、20 D、248. 若关于 的分式方程 的解为正数,则满足条件的正整数 的值为( )A、 B、 C、 D、9. 如图,在中, , 为内一点,过点的直线分别交、于点 , , 若在的垂直平分线上,在的垂直平分线上,则的度数为( ) A、 B、 C、 D、10. 如图,在中, , , . 、分别平分 , , 则的长为( )
A、 B、 C、 D、10. 如图,在中, , , . 、分别平分 , , 则的长为( )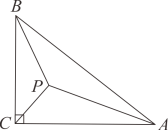 A、 B、 C、4 D、2
A、 B、 C、4 D、2二、填空题
-
11. 分式: , , 的最简公分母是 .12. 正六边形的一个内角是正n边形一个外角的4倍,则n= .13. 已知点 , 将点沿水平方向向左平移个单位后落在轴上,则点的坐标为 .14. 如图,点 , 分別是的边 , 的中点,连接 , 过点作交的延长线于点 , 若 , 则的长为 .
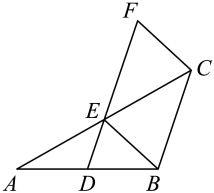 15. 已知一次函数的图象经过第一、二、四象限,且与轴交于点 , 则关于的不等式的解集为 .16. 如图,点 , 分别在等边的边、上,将沿直线翻折,使点落在处, , 分別交边于点 , , 若 , 则的度数为 .
15. 已知一次函数的图象经过第一、二、四象限,且与轴交于点 , 则关于的不等式的解集为 .16. 如图,点 , 分别在等边的边、上,将沿直线翻折,使点落在处, , 分別交边于点 , , 若 , 则的度数为 .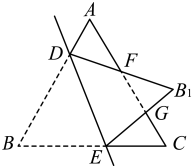 17. 某传染病传播期间为尽快完成病人检测任务,某地组织甲、乙两支医疗队,分別开展检测工作,甲队比乙队每小时多检测人,甲队检测人,比乙队检测人所用的时间少 , 则甲队每小时检测的人数是人.18. 如图,四边形中, , . , 若 , 则的长为 .
17. 某传染病传播期间为尽快完成病人检测任务,某地组织甲、乙两支医疗队,分別开展检测工作,甲队比乙队每小时多检测人,甲队检测人,比乙队检测人所用的时间少 , 则甲队每小时检测的人数是人.18. 如图,四边形中, , . , 若 , 则的长为 .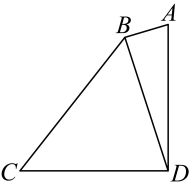
三、解答题
-
19.(1)、解方程:(2)、解不等式组: , 并把解集在数轴上表示出来.20. 先化简 , 再从 , , 中选择合适的值代入求值.21. 如图,是上一点,于点 , 于点 . , 分别是 , 上的点. , .
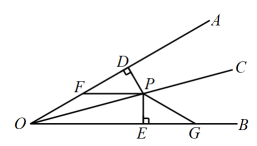 (1)、求证:是的平分线;(2)、若 , , . 求的长.22. 如图,在平面直角坐标系中,的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)、求证:是的平分线;(2)、若 , , . 求的长.22. 如图,在平面直角坐标系中,的三个顶点分别是A(1,3),B(4,4),C(2,1).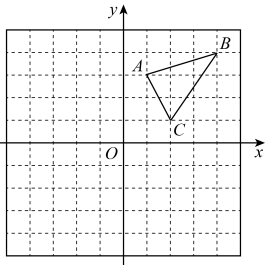 (1)、把向左平移4个单位后得到对应的 , 请画出平移后的;(2)、把绕原点旋转180°后得到对应的 , 请画出旋转后的;(3)、观察图形,判断与是否成中心对称?如果是,直接写出对称中心的坐标.23. 某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)、把向左平移4个单位后得到对应的 , 请画出平移后的;(2)、把绕原点旋转180°后得到对应的 , 请画出旋转后的;(3)、观察图形,判断与是否成中心对称?如果是,直接写出对称中心的坐标.23. 某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)、求甲、乙两种树苗每棵的价格各是多少元?
(2)、在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
24. 如图,四边形是平行四边形,的平分线交于点 , 交的延长线于点 .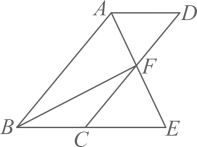 (1)、求证:为等腰三角形;(2)、连接 , 若 , , , 求平行四边形的面积.25. 为了号召市民向贫困山区的孩子捐赠衣物,某校八(1)班的同学准备发倡议书,倡议书的制作有两种方案可供选择:
(1)、求证:为等腰三角形;(2)、连接 , 若 , , , 求平行四边形的面积.25. 为了号召市民向贫困山区的孩子捐赠衣物,某校八(1)班的同学准备发倡议书,倡议书的制作有两种方案可供选择:方案一:由复印店代做,所需费用与倡议书张数满足如图①所示的函数关系;
方案二:租货机器自己制作,所需费用(包括租赁机器的费用和制作倡议书费用)与倡议书张数满足如图②所示的函数关系;
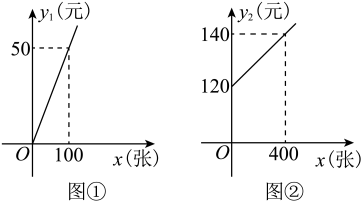 (1)、直接写出方案一中每张倡议书的价格;(2)、请分別求出 , 关于的函数关系式;(3)、从省钱的角度看,如何选择制作方案.26. 某数学托管兴趣小组对图形的旋转进行了如下探究:
(1)、直接写出方案一中每张倡议书的价格;(2)、请分別求出 , 关于的函数关系式;(3)、从省钱的角度看,如何选择制作方案.26. 某数学托管兴趣小组对图形的旋转进行了如下探究: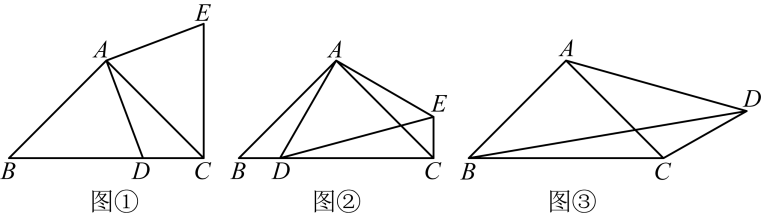 (1)、【特例发现】
(1)、【特例发现】如图①,在中, , , 为边上一点(不与点、重合),将线段绕点逆时针旋转得到 , 连接 , 试探索线段 , , 之间满足的等量关系,并证明你的结论;
(2)、【类比探究】如图②,在与中, , , , , 将绕点旋转,使点落在边上,连接 , 试探索线段 , , 之间满足的等量关系,并证朋你的结论;
(3)、【迁移应用】如图③,在四边形中, . 若 , , 求的长