江西省赣州市寻乌县2022-2023学年八年级下学期数学期末考试试卷

试卷更新日期：2023-07-31 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{a - 1}$ 在实数范围内有意义，则 $a$ 的取值范围是（）

A、 $a \geq 0$ B、 $a \geq 1$ C、 $a \leq 1$ D、 $a \leq - 1$

查看试题解析
2. 下列各组数中，不是勾股数的一组是（）

A、3，4，5 B、4，5，6 C、6，8，10 D、5，12，13

查看试题解析
3. 在一次统计调查中，小明得到以下一组数据： $3 ， 4 ， x ， 5 ， 6$ ，若这组数据的众数是3，则这组数据中的 $x$ 的值为（）

A、4 B、 $3.5$ C、3 D、5

查看试题解析
4.
在平面直角坐标系中，一次函数y=kx+b的图象如图所示，观察图象可得（）

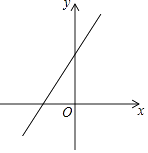A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
5. 如图，在矩形 $A B C D$ 中，对角线 $A C ､ B D$ 相交于点 $O$ ，点 $E ､ F$ 分别是 $A O ､ A D$ 的中点，连接 $E F$ ，若 $A B = 6 ， B C = 8$ ，则 $E F$ 的长是（）

A、5 B、2 C、2.5 D、3

查看试题解析
6. 在学校开展的节约用水活动中，从八年级600名同学中随机调查了30名同学的家庭一个月的节水量，数据（均为正整数）整理如表：请你估计这600名同学的家庭一个月节约用水的总量大约是（    ）
月节水量 $x / t$
人数
          $1.5 \leq x < 2.5$
6
          $2.5 \leq x < 3.5$
15
          $3.5 \leq x < 4.5$
9

A、 $3.1 t$ B、 $93 t$ C、 $930 t$ D、 $1860 t$

查看试题解析

二、填空题

7. 若函数 $y = 3 x^{m - 2}$ 是正比例函数，则 $m$ 的值是．

查看试题解析
8. 若 $\sqrt{5}$ 与最简二次根式 $\sqrt{a + 1}$ 是同类二次根式，则 $a =$ ．

查看试题解析
9. 学校组织一分钟跳绳比赛．八（1）班准备从甲、乙两人中挑选一名成绩比较稳定的同学参赛．两人最近四次的跳绳测试的成绩（单位：个）为：甲：197，213，209，196；乙：205，203，202，205，而这两人平均成绩相同，根据信息，应该选参加比赛．

查看试题解析
10. 《九章算术》中记载：今有立木，系索其末，委地三尺，引索却行，去本八尺而索尽．问索长几何．译文：今有一竖直着的木柱，在木柱的上端系有绳索，绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺（绳索比木柱长 $3$ 尺），牵着绳索退行，在距木柱底部 $8$ 尺处时而绳索用尽．设绳索长为 $x$ 尺，则根据题意可列方程为．

查看试题解析
11. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $B (m ， 0) (m > 1)$ ，与正比例函数 $y = 2 x$ 的图象交于点 $A$ ，则不等式 $k x + b < 2 x$ 的解集为．

查看试题解析
12. 小亮在一张长为 $9 c m$ ，宽为 $8 c m$ 的矩形纸片上，剪了一个腰长为 $5 c m$ 的等腰三角形（要求等腰三角形的一个顶点与矩形的一个顶点重合，其余两个顶点在矩形的边上），则这个等腰三角形的底边为 $c m$ ．

查看试题解析

三、解答题

13.

(1)、计算： $\begin{matrix} (3 \sqrt{12} - 6 \sqrt{\frac{1}{3}}) \div \sqrt{3} \end{matrix}$

(2)、已知小玲的饭卡里存有100元钱，她每餐吃饭的费用为7元．设吃饭的餐数为x餐，饭卡里剩下的钱为y元．
①y与x之间的函数关系式是： ▲ ．（不用写自变量的取值范围）；
②求当 $x = 8$ 时，y的值．

查看试题解析
14. 数学老师在计算学生的学期综合成绩时，从平时作业、期中考试、期末考试三个方面进行考核，各项满分均为100分．按平时作业占20%，期中考试占40%，期末考试占40%．小华和小强两位同学的成绩如下表所示，则：
学生
平时作业
期中考试
期末考试
小华
80
80
88
小强
75
80
92

(1)、这两人中综合成绩更高的同学是成绩是，他的综合分．

(2)、若对平时作业、期中考试、期末考试的成绩分别赋予它们2，3和5的权，请计算小华的综合成绩．

查看试题解析
15. 为了绿化校园．学校计划在如图所示的一块四边形 $A C B D$ 的空地（图中阴影部分）上种植草皮，经测量 $∠ A C B = 90 ° ， B C = 3 m ， A C = 4 m ， B D = 12 m ， A D = 13 m$ ，请求出空地的面积．

查看试题解析
16. 如图是 $7 \times 8$ 的矩形网格，每个小正方形的顶点称为格点，请仅用无刻度直尺按下列要求作图，所作图形的顶点均在格点上（保留作图痕迹）．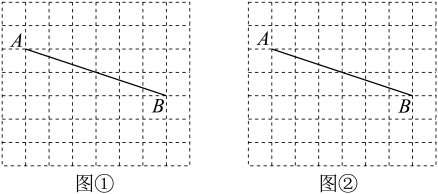

(1)、在图①中，作一个以 $A B$ 为一边而且面积为18的平行四边形 $A B C D$ ；

(2)、在图②中，作一个以 $A B$ 为其中一条对角线的正方形 $A E B F$ ．

查看试题解析
17. 已知小王家、体育中心、新华书店在同一直线上．如图所示的图象反映的过程是：小王骑电动车从家出发去体育中心锻炼身体．当他骑了一段路时，突然想起要帮弟弟买书，于是原路返回到刚才经过的新华书店（不考虑电动车掉头的时间），买到书后继续前进并到达体育中心．请根据图象回答下列问题：

(1)、体育中心到小王家的距离是米．

(2)、第20分钟时，他在（地点），他在这个地方停留了分钟．

(3)、买到书后，小王从新华书店到体育中心骑车的平均速度是多少？

查看试题解析
18. 如图， $D B ∥ A C ， A C = 2 D B ， E$ 是 $A C$ 的中点．

(1)、求证： $D E = B C$ ；

(2)、连接 $A D ､ B E$ ，在不添加辅助线的情况下，请直接写出与 $△ A B D$ 面积相等的所有三角形．

查看试题解析
19. 一本好书往往能改变人的一生，在学校组织的“读书周”活动期间，同学们掀起了读书的热潮．各班读书的同学越来越多了，同学们的阅读量也增加了不少．下面是小欢同学调查的八（8）班全体同学在“读书周”活动期间阅读图书的册数情况统计图：

请你根据以上统计图中的信息，解答下列问题：

(1)、该班有学生人．

(2)、请补全条形统计图；

(3)、这组数据的中位数是多少？

(4)、若该校共有4000名学生，请你估计这个学校阅读了5册图书的学生人数．

查看试题解析
20. 观察下列含有规律的式子：①． $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ， ②． $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ， ③． $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ， …根据你发现的规律，完成下面各题：

(1)、按照这个规律，写出第④个式子：；

(2)、若式子 $\sqrt{a + \frac{1}{b}} = 8 \sqrt{\frac{1}{b}}$ （ $a ､ b$ 为正整数）符合以上规律，则 $\sqrt{a + b} =$ ；

(3)、请你用含有正整数 $n$ 的式子，表示出你所发现的规律：；

(4)、请你通过计算，验证：当 $n = 20$ 时，对应的式子是正确的．

查看试题解析
21. 如图，是一种学生双肩背包，其背带由固定带、活动带和调节扣构成．使用时，可以通过调节调节扣使背带的总长度（固定带与活动带使用部分的长度总和，其中调节扣所占的长度忽略不计）加长或缩短．设活动带未使用部分的长度为xcm，背带的总长度为ycm，经测量，得到如下数据：（说明：本题只讨论一条背带）
活动带未使用部分的长度 $x (c m)$
5
10
15
20
          $⋯$
30
背带的总长度 $y (c m)$
65
60
55
          $m$
          $⋯$
          $n$


(1)、根据表中数据的规律，填空： $m =$ ， $\begin{matrix} n = \end{matrix}$ ．

(2)、当 $5 \leq x \leq 30$ 时，求 $y$ 关于 $x$ 的函数解析式．

(3)、在上面的平面直角坐标系中，请直接画出（2）中的函数图象；

(4)、根据小敏的身高和习惯，背带的总长度为 $52 c m$ 时，背起来最合适，请求出此时活动带未使用部分的长度．

查看试题解析
22. 如图，直线 $y = k x + b (k \neq 0)$ 交两坐标轴于点 $A (4 ， 0) ， B (0 ， 3)$ ．

(1)、求直线 $y = k x + b$ 的解析式；

(2)、点 $C$ 的坐标为 $(- 3 ， - 1)$ ，连接 $B C$ ．证明： $A B ⊥ B C$ ，且线段 $A B = B C$ ；

(3)、在（2）的条件下，点 $D$ 为平面直角坐标系内一点，当四边形 $A B C D$ 为正方形时，请直接写出点 $D$ 的坐标．

查看试题解析
23. 【问题背景】在学完菱形的知识之后，小彬对菱形进行了研究：如图，在菱形 $A B C D$ 中， $∠ A B C = 60 ° ， E$ 是射线 $A C$ 上一点， $F$ 是 $B C$ 的延长线上一点，且 $C F = A E$ ，连接 $B E ， E F$ ．

(1)、【问题发现】如图1，当 $E$ 是对角线 $A C$ 的中点时，小彬发现有： $B E = E F$ ．请你证明他的发现是正确的．

(2)、【类比探究】如图2，若 $E$ 是对角线 $A C$ 上任意一点时，问题（1）中的结论是否还成立？请说明理由．

(3)、【拓展应用】如图3，若 $E$ 是线段 $A C$ 延长线上任意一点，连接 $A F$ ，其他条件不变， $∠ 1 = 30 ° ， A B = 2$ ，请求出 $A F$ 的长度．

查看试题解析

月节水量 $x / t$	人数
$1.5 \leq x < 2.5$	6
$2.5 \leq x < 3.5$	15
$3.5 \leq x < 4.5$	9

学生	平时作业	期中考试	期末考试
小华	80	80	88
小强	75	80	92

活动带未使用部分的长度 $x (c m)$	5	10	15	20	$⋯$	30
背带的总长度 $y (c m)$	65	60	55	$m$	$⋯$	$n$