江西省新余市分宜县2022-2023学年八年级下学期数学期末考试试卷
试卷更新日期:2023-07-31 类型:期末考试
一、单选题
-
1. 以下图形既是轴对称图形,又是中心对称图形的是( )A、等腰三角形 B、平行四边形 C、矩形 D、等边三角形2. 已知两组数据x1 , x2 , x3和x1+1,x2+1,x3+1,则这两组数据没有改变大小的统计量是( )A、平均数 B、中位数 C、众数 D、方差3. 如图,已知在平面直角坐标系中,四边形ABCD是菱形,其中点B坐标是(4,1),点D坐标是(0,1),点A在x轴上,则菱形ABCD的周长是( )
 A、8 B、2 C、4 D、124. 如图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是( )
A、8 B、2 C、4 D、124. 如图,平面直角坐标系中,在边长为1的正方形的边上有一动点沿运动一周,则的纵坐标与点走过的路程之间的函数关系用图象表示大致是( ) A、
A、 B、
B、 C、
C、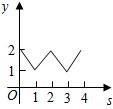 D、
D、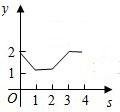 5. 如图,在长方体盒子中,已知 , 长为的细直木棒恰好从小孔G处插入,木棒的一端I与底面接触,当木棒的端点I在长方形内及边界运动时,长度的最小值为( )
5. 如图,在长方体盒子中,已知 , 长为的细直木棒恰好从小孔G处插入,木棒的一端I与底面接触,当木棒的端点I在长方形内及边界运动时,长度的最小值为( )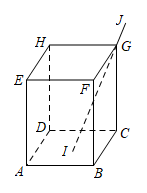 A、 B、 C、 D、6. 如图,正方形的边长为6,点是上的一点,连接并延长,交射线于点 , 将沿直线翻折,点落在点处,的延长线交于点 , 当时,则的长为( )
A、 B、 C、 D、6. 如图,正方形的边长为6,点是上的一点,连接并延长,交射线于点 , 将沿直线翻折,点落在点处,的延长线交于点 , 当时,则的长为( )
 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
7. 在平面镜中看到一辆汽车的车牌号:
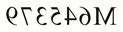 ,则该汽车的车牌号是 . 8. 若 , 都是实数, , 则的值为 .9. 已知x= +1,则x2﹣2x﹣3= .10. 如图,直线与轴、轴分别交于点和点 , 点、分别为线段、的中点,点为上一动点,当最小时,点的坐标为 .
,则该汽车的车牌号是 . 8. 若 , 都是实数, , 则的值为 .9. 已知x= +1,则x2﹣2x﹣3= .10. 如图,直线与轴、轴分别交于点和点 , 点、分别为线段、的中点,点为上一动点,当最小时,点的坐标为 . 11. 如图所示的网格是正方形网格,点、、、、是网格线交点,则的为度.
11. 如图所示的网格是正方形网格,点、、、、是网格线交点,则的为度. 12. 在中, , 有一个锐角为 , , 若点在直线上(不与点 , 重合),且 , 则的长为 .
12. 在中, , 有一个锐角为 , , 若点在直线上(不与点 , 重合),且 , 则的长为 .三、解答题
-
13.(1)、计算:;(2)、先化简,再求值: , 其中为满足的整数.14. 如图,在边长为的等边中,、分别为、的中点,于点 , 为的中点,连接 .
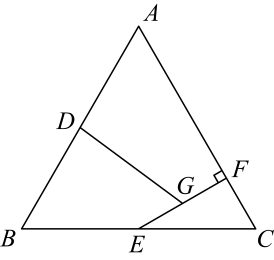 (1)、求的长.(2)、求的长.15. 阅读下列材料解答问题:新定义:对非负数“四舍五入”到个位的值记为 , 即:当为非负整数时,如果 , 则;反之,当为非负整数时,如果 , 则 . 例如: , , , , …,试解决下列问题:(1)、①(为圆周率);
(1)、求的长.(2)、求的长.15. 阅读下列材料解答问题:新定义:对非负数“四舍五入”到个位的值记为 , 即:当为非负整数时,如果 , 则;反之,当为非负整数时,如果 , 则 . 例如: , , , , …,试解决下列问题:(1)、①(为圆周率);②如果 , 则数的取值范围为;
(2)、求出满足的的取值范围.16. 已知正方形 , 是的中点,请仅用无刻度的直尺按下列要求画图.(保留画图痕迹,不写画法) (1)、在图①中,画 , 垂足为;(2)、在图②中,画 , 垂足为 .17. 如图,为 , 过点的一次函数的图象与正比例函数的图象相交于点 .
(1)、在图①中,画 , 垂足为;(2)、在图②中,画 , 垂足为 .17. 如图,为 , 过点的一次函数的图象与正比例函数的图象相交于点 . (1)、求该一次函数的解析式.(2)、该一次函数与轴交于点 , 若点为直线上的动点,当面积等于面积的时,求点的坐标.18. 如图,已知 , , 为轴正半轴上一点,点为第二象限一动点,在的延长线上,交于 , 且 .
(1)、求该一次函数的解析式.(2)、该一次函数与轴交于点 , 若点为直线上的动点,当面积等于面积的时,求点的坐标.18. 如图,已知 , , 为轴正半轴上一点,点为第二象限一动点,在的延长线上,交于 , 且 .
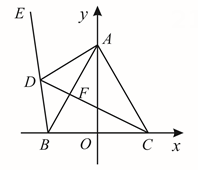 (1)、求证:平分;(2)、若在点运动的过程中,始终有 , 在此过程中,的度数是否变化?如果变化,请说明理由;如果不变,请求出的度数?19. 星火体育用品店销售甲、乙两种品牌篮球,其中甲品牌篮球的进价为90元/个,售价为130元/个,乙品牌进价为70元/个,售价为100元/个.现计划用不超过8080元购进甲、乙两种品牌篮球共92个,其中甲品牌篮球不少于58个,设购进甲品牌篮球个,总利润为元.(1)、求甲品牌篮球最多购进多少个?(2)、该体育用品店对甲品牌篮球每个降价元,乙品牌篮球价格不变,如果这92个篮球全部售完,那么该店如何进货才能获得最大利润?20. 观察下列各式.
(1)、求证:平分;(2)、若在点运动的过程中,始终有 , 在此过程中,的度数是否变化?如果变化,请说明理由;如果不变,请求出的度数?19. 星火体育用品店销售甲、乙两种品牌篮球,其中甲品牌篮球的进价为90元/个,售价为130元/个,乙品牌进价为70元/个,售价为100元/个.现计划用不超过8080元购进甲、乙两种品牌篮球共92个,其中甲品牌篮球不少于58个,设购进甲品牌篮球个,总利润为元.(1)、求甲品牌篮球最多购进多少个?(2)、该体育用品店对甲品牌篮球每个降价元,乙品牌篮球价格不变,如果这92个篮球全部售完,那么该店如何进货才能获得最大利润?20. 观察下列各式.…
请根据你发现的规律完成下列各题:
(1)、根据规律可得;(其中为正整数)(2)、计算: . (结果保留幂的形式)(3)、计算: . (结果保留幂的形式)21. 最近,由于甲市疫情严重,全国各地纷纷支援,乙市积极开展爱心物资捐赠活动,并派遣志愿者去甲市服务.某日,装满物资的货车比乘载志愿者的客车提前半小时出发,它们离乙市的距离y(km)与货车行驶的时间x(h)之间的函数图象如图所示.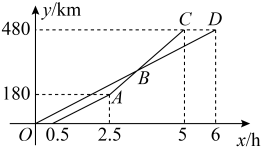 (1)、甲、乙两市之间的距离为 , 货车的速度为;(2)、请求出段与之间的函数关系式及点的坐标,并解释交点的实际意义;(3)、请直接写出在客车行驶过程中两车相距时对应的值.22.(1)、如图1, , .若a,b满足 ,求A、B的坐标.
(1)、甲、乙两市之间的距离为 , 货车的速度为;(2)、请求出段与之间的函数关系式及点的坐标,并解释交点的实际意义;(3)、请直接写出在客车行驶过程中两车相距时对应的值.22.(1)、如图1, , .若a,b满足 ,求A、B的坐标. (2)、在(1)的条件下,点C为线段AB上的一点, , ,垂足分别为E、F、若 , , ,求线段EF的长.(3)、如图2, , ,点P为 的角平分线的交点,若a,b满足 , 交x轴于N,延长OP交AB于M,直接写出AB、ON、PM之间的数量关系(不需要写出证明过程).
(2)、在(1)的条件下,点C为线段AB上的一点, , ,垂足分别为E、F、若 , , ,求线段EF的长.(3)、如图2, , ,点P为 的角平分线的交点,若a,b满足 , 交x轴于N,延长OP交AB于M,直接写出AB、ON、PM之间的数量关系(不需要写出证明过程). 23. 我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.(1)、在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美"四边形的是(请填序号);(2)、在“完美”四边形中, , , 连接 .
23. 我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.(1)、在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美"四边形的是(请填序号);(2)、在“完美”四边形中, , , 连接 .

①如图1,求证:平分;
小明通过观察、实验,提出以下两种想法,证明平分:
想法一:通过 , 可延长到 , 使 , 通过证明 , 从而可证平分;
想法二:通过 , 可将绕点顺时针旋转,使与重合,得到 , 可证 , , 三点在一条直线上,从而可证平分 .
请你参考上面的想法,选择其中一种想法帮助小明证明平分;
②如图2,当时,用等式表示线段 , , 之间的数量关系,并证明.