四川省雅安市2023年中考数学真题
试卷更新日期:2023-07-31 类型:中考真卷
一、单选题
-
1. 在0, , , 2四个数中,负数是( )A、0 B、 C、 D、22. 计算的结果是( )A、 B、0 C、1 D、193. 如图,是由3个相同的小正方体搭成的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图, , 于点C, , 则的度数为( )
4. 如图, , 于点C, , 则的度数为( ) A、 B、 C、 D、5. 若 . 则的值是( )A、 B、 C、5 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 不等式组的解集是( )A、 B、 C、 D、8. 如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得 , , , 则种草区域的面积为( )
A、 B、 C、 D、5. 若 . 则的值是( )A、 B、 C、5 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 不等式组的解集是( )A、 B、 C、 D、8. 如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得 , , , 则种草区域的面积为( ) A、 B、 C、 D、9. 某位运动员在一次射击训练中,次射击的成绩如图,则这10次成绩的平均数和中位数分别是( )
A、 B、 C、 D、9. 某位运动员在一次射击训练中,次射击的成绩如图,则这10次成绩的平均数和中位数分别是( )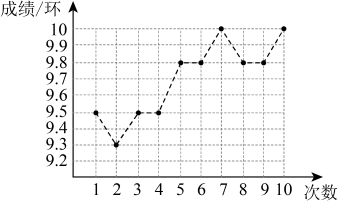 A、 , B、 , C、 , D、 ,10. 在平面直角坐标系中.将函数的图象绕坐标原点逆时针旋转 , 再向上平移1个单位长度,所得直线的函数表达式为( )A、 B、 C、 D、11. 如图,在中,F是上一点,交于点E,的延长线交的延长线于点G, , , 则的长为( )
A、 , B、 , C、 , D、 ,10. 在平面直角坐标系中.将函数的图象绕坐标原点逆时针旋转 , 再向上平移1个单位长度,所得直线的函数表达式为( )A、 B、 C、 D、11. 如图,在中,F是上一点,交于点E,的延长线交的延长线于点G, , , 则的长为( ) A、4 B、6 C、8 D、1012. 如图,二次函数的图象与x轴交于 , B两点,对称轴是直线 , 下列结论中,①;②点B的坐标为;③;④对于任意实数m,都有 , 所有正确结论的序号为( )
A、4 B、6 C、8 D、1012. 如图,二次函数的图象与x轴交于 , B两点,对称轴是直线 , 下列结论中,①;②点B的坐标为;③;④对于任意实数m,都有 , 所有正确结论的序号为( ) A、①② B、②③ C、②③④ D、③④
A、①② B、②③ C、②③④ D、③④二、填空题
-
13. 在一个不透明的口袋中,装有1个红球若干个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为 , 则此口袋中白球的个数为.14. 若 , , 则的值为 .15. 已知关于x的方程的一个根为1,则该方程的另一个根为 .16. 如图,在中, . P为边上一动点,作于点D,于点E,则的最小值为 .
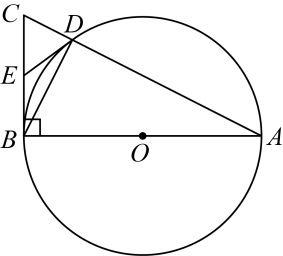
 17. 如图.四边形中, , , , 交于点 , , , 则AB的长为 .
17. 如图.四边形中, , , , 交于点 , , , 则AB的长为 .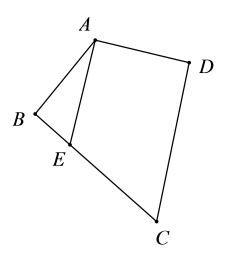
三、解答题
-
18.(1)、计算:(2)、先化简,再求值: . 其中19. 某校为了调查本校学生对航空航天知识的知晓情况.开展了航空航天知识竞赛,从参赛学生中,随机抽取若干名学生的成绩进行统计,得到如下不完整的统计图表:
成绩/分
频数/人
频率
10
0.1
15
b
a
0.35
40
c
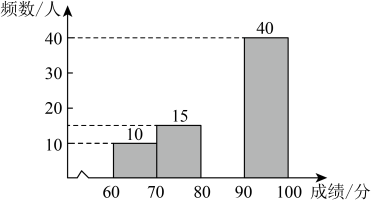
请根据图表信息解答下列问题:
(1)、求a,b,c的值;(2)、补全频数直方图;(3)、某班有2名男生和1名女生的成绩都为100分,若从这3名学生中随机抽取2名学生参加演讲,用列表或画树状图的方法,求抽取的2名学生恰好为1男1女的概率.20. 如图,已知 , 是对角线上两点, . (1)、求证:;(2)、若交的延长线于点 , , 求的面积.21. 李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:
(1)、求证:;(2)、若交的延长线于点 , , 求的面积.21. 李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:品名
甲蔬菜
乙蔬菜
批发价/(元/kg)
零售价/(元/kg)
(1)、若他批发甲、乙两种蔬菜共花元.求批发甲乙两种蔬菜各多少千克?(列方程或方程组求解)(2)、若他批发甲、乙两种蔬菜共花m元,设批发甲种蔬菜 , 求m与n的函数关系式;(3)、在(2)的条件下,全部卖完蔬菜后要保证利润不低于元,至少批发甲种蔬菜多少千克?22. 如图,在平面直角坐标系中,四边形是边长为的正方形.点 , 在坐标轴上.反比例函数的图象经过点 . (1)、求反比例函数的表达式;(2)、点D在反比例函数图象上,且横坐标大于2, . 求直线的函数表达式.
(1)、求反比例函数的表达式;(2)、点D在反比例函数图象上,且横坐标大于2, . 求直线的函数表达式.