2023-2024学年北师大版数学九年级上册4.7相似三角形的性质(提升卷)
试卷更新日期:2023-07-31 类型:同步测试
一、选择题
-
1. 如图所示, , , , 则的长为( )
 A、 B、2 C、3 D、42. 已知 , 且.若的周长为8,则的周长是( )A、4 B、8 C、12 D、183. 如果两个相似三角形的面积之比为9:4,那么这两个三角形对应边上的高之比为( )A、9:4 B、3:2 C、2:3 D、81:164. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
A、 B、2 C、3 D、42. 已知 , 且.若的周长为8,则的周长是( )A、4 B、8 C、12 D、183. 如果两个相似三角形的面积之比为9:4,那么这两个三角形对应边上的高之比为( )A、9:4 B、3:2 C、2:3 D、81:164. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( ) A、AC2=AD•AB B、BC2=BD•BA C、CD2=AD•DB D、CD2=CA•CB5. 已知△ABC∽△A'B'C,AD和A'D'是它们的对应高线,若AD=4,A'D'=1,则△ABC与△A'B'C的面积比是( )A、16:1 B、4:1 C、4:3 D、4:96. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 , 另一个三角形的最短边长为 , 则它的最长边为( )A、 B、 C、 D、7. 已知,△ABC∽△A′B′C′,且△A′B′C′的面积为6,△A′B′C′周长是△ABC的周长的 , AB=8,则AB边上的高等于( )A、3 B、6 C、9 D、128. 已知△ABC∽△DEF,AB:DE=3:1,AC=6,则DF为( )A、18 B、2 C、54 D、9. 如图,在正方形网格中,、的顶点都在正方形网格的格点上, , 则的度数为( )
A、AC2=AD•AB B、BC2=BD•BA C、CD2=AD•DB D、CD2=CA•CB5. 已知△ABC∽△A'B'C,AD和A'D'是它们的对应高线,若AD=4,A'D'=1,则△ABC与△A'B'C的面积比是( )A、16:1 B、4:1 C、4:3 D、4:96. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 , 另一个三角形的最短边长为 , 则它的最长边为( )A、 B、 C、 D、7. 已知,△ABC∽△A′B′C′,且△A′B′C′的面积为6,△A′B′C′周长是△ABC的周长的 , AB=8,则AB边上的高等于( )A、3 B、6 C、9 D、128. 已知△ABC∽△DEF,AB:DE=3:1,AC=6,则DF为( )A、18 B、2 C、54 D、9. 如图,在正方形网格中,、的顶点都在正方形网格的格点上, , 则的度数为( ) A、30° B、45° C、60° D、75°10. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
A、30° B、45° C、60° D、75°10. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( ) A、= B、= C、= D、=
A、= B、= C、= D、=二、填空题
-
11. 如图,D、E分别是ΔABC的边AB、AC上的动点,若 , 且ΔADE与ΔABC相似,则AD的长度是.
 12. 若 , 它们的面积比为 , 则它们的对应高的比为 .13. 如图,、交于点 , 且 , , , 当时,与相似.
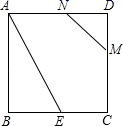
12. 若 , 它们的面积比为 , 则它们的对应高的比为 .13. 如图,、交于点 , 且 , , , 当时,与相似. 14. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为.
14. 如图,正方形的边长为6,点F为的中点,点E在上,且 , 在边上找一点P,使以E,D,P为顶点的三角形与相似,则的长为. 15. 如图,点在等边三角形的边上,连接 , 线段的垂直平分线分别交边 , 于点 , 当时,的值为 .
15. 如图,点在等边三角形的边上,连接 , 线段的垂直平分线分别交边 , 于点 , 当时,的值为 .
三、解答题
-
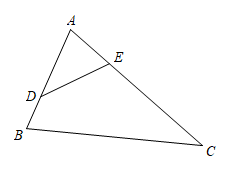
16. 如图所示,点D、E分别在AB、AC上,连接DE,△ADE∽△ABC,已知△ADE和△ABC的相似比是1:2,且△ADE的面积是1,求四边形DBCE的面积.
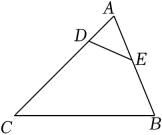
 17. 如图,分别是、上的点, , , , , , 求的长和的度数.
17. 如图,分别是、上的点, , , , , , 求的长和的度数.