2023-2024学年北师大版数学九年级上册4.7相似三角形的性质（基础卷）

试卷更新日期：2023-07-31 类型：同步测试

进入出卷网下载

一、选择题

1. 两个相似三角形的相似比是4：9，则它们的面积比是（）

A、4：9 B、16：81 C、2：3 D、1：3

查看试题解析
2. 将 $△ A B C$ 放大到2倍，得到 $△ A^{'} B^{'} C^{'}$ ，则 $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 的面积比是（）

A、 $1 ： 2$ B、 $1 ： 3$ C、 $1 ： 4$ D、 $1 ： 5$

查看试题解析
3. 已知 $△ A B C ∽ △ D E F$ ， $A G$ 和 $D H$ 是它们的对应边上的高，若 $A G = 4$ ， $D H = 6$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比是（）

A、2：3 B、4：9 C、3：2 D、9：4

查看试题解析
4. 如图，在直角梯形 $A B C D$ 中， $∠ A B C = 90 °$ ， $A B = 8$ ， $A D = 3$ ， $B C = 4$ ，点 $P$ 为边 $A B$ 上一动点，若 $△ P A D$ 与 $△ P B C$ 是相似三角形，则满足条件的点 $P$ 的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 如图，一块等腰直角三角板，它的斜边BC=8cm，内部△DEF的各边与OABC的各边分别平行，且它的斜边EF=4cm，则△DEF的面积与阴影部分的面积比为（）

A、1：2 B、1：3 C、1：4 D、1：8

查看试题解析
6. 若两个相似三角形的面积之比为1：4，则它们的最长边的比是（）

A、1：2 B、1：4 C、1：16 D、无法确定

查看试题解析
7. 已知 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ ，如果 $A C = 6$ ， $A^{'} C^{'} = 2.4$ ，那么 $△ A^{'} B^{'} C^{'}$ 与 $△ A B C$ 的周长比为（　　）

A、3：2 B、3：4 C、2：5 D、5：2

查看试题解析
8. 已知 $△$ ABO∽ $△$ DEO，且BO：EO＝1：3，则△ABO与△DEO的面积比是（）

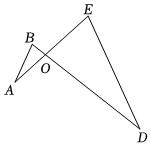A、1：3 B、3：1 C、1：9 D、9：1

查看试题解析
9. 如图，已知△ABC∽△DEF，若∠A＝35°，∠B＝65°，则∠F的度数是（）

A、30° B、35° C、80° D、100°

查看试题解析
10. 若两个相似三角形的相似之比为1：2，则它们的面积之比为（）

A、1：2 B、1：4 C、1：5 D、1：16

查看试题解析

二、填空题

11. 如果两个相似三角形的面积比为3：4，那么它们对应高之比为．

查看试题解析
12. 如果两个相似三角形的周长比是1︰4，那么它们的面积比是.

查看试题解析
13. 若 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ ， $\frac{A B}{A^{'} B^{'}} = \frac{3}{4}$ ， $△ A B C$ 的面积为 $3 {cm}^{2}$ ，则 $△ A^{'} B^{'} C^{'}$ 的面积为 ${cm}^{2}$ .

查看试题解析
14. 已知△ABC∽△DEF，AB=3DE，△ABC的周长是12，则△DEF的周长为．

查看试题解析
15. 若D为 $△ A B C$ 中 $A B$ 边上一点，且ED $∥$ BC交 $A C$ 于E， $A B = 6 ， B C = 8 ， A C = 10$ ，若 $△ A D E$ 与 $△ A B C$ 的相似比为 $\frac{1}{2}$ ，则 $A E =$ .

查看试题解析

三、解答题

16. 如图，已知△ABC∽△ADE，AB＝15，BD＝3，BC＝12，求DE的长．

查看试题解析
17. 如图，已知 $△ A B C$ 中， $A B = 8$ ， $B C = 7$ ， $A C = 6$ ，点 $D$ 、 $E$ 分别在 $A B$ 、 $A C$ 上，如果以 $A$ 、 $D$ 、 $E$ 为顶点的三角形和 $△ A B C$ 相似，且相似比为 $\frac{1}{4}$ ，试求 $A D$ 、 $A E$ 的长．

查看试题解析
18.
已知：如图，△ABC∽△ADE ， ∠A=45°，∠C=40°．求：∠ADE的度数．

查看试题解析
19. 一个三角形三边长分别为5cm，8cm，12cm，另一个与它相似的三角形的最长边为4.8cm，求另外两边长．

查看试题解析
20. 如图，在Rt△ABC中，∠A=90º，AB=6，BC=10，D是AC上一点，CD=5，DE⊥BC于E.求线段DE的长.

查看试题解析