2023-2024学年北师大版数学九年级上册4.6利用相似三角形测高（基础卷）
试卷更新日期：2023-07-31 类型：同步测试
一、选择题
-
1. 如图，它是物理学中小孔成像的原理示意图，已知物体 ， 根据图中尺寸 ， 则的长应是（ ）
A、15 B、30 C、20 D、102. 如图所示，某校数学兴趣小组利用标杆BE测量物的高度，已知标杆BE高1.5m，测得AB＝1.2m，AC＝14m，则建筑物CD的高是（ ）
A、17.5m B、17m C、16.5m D、18m3. 如图，为估算学校的旗杆的高度，身高 米的小红同学沿着旗杆在地面的影子 由 向 走去，当她走到点 处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得 ， ，则旗杆的高度是（ ）
A、6.4m B、7m C、8m D、9m4. 如图，利用标杆BE测量建筑物的高度.已知标杆BE高1.2m，AB：AC=1：9，则建筑物CD的高是（ ）
A、9.6m B、10.8m C、12m D、14m5. 如图，放映幻灯片时，通过光源，把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm，光源到屏幕的距离为90cm，且幻灯片中的图形的高度为7cm，则屏幕上图形的高度为（ ）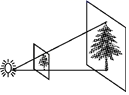
A、21cm B、14cm C、6cm D、24cm6. 学校门口的栏杆如图所示，栏杆从水平位置 绕 点旋转到 位置，已知 ， ，垂足分别为 ， ， ， ， ，则栏杆 端应下降的垂直距离 为（ ）
A、
B、
C、
D、
7. 如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上。若测得BE=20m，EC=10m，CD=20m，则河的宽度AB等于（ ）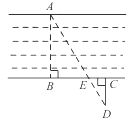
A、60m B、40m C、30m D、20m8. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交DB于点F，则△DEF的面积与△BAF的面积之比为（ ）
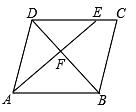A、1：3 B、3：4 C、1：9 D、9：169. 为测量某河的宽度，小军在河对岸选定一个目标点A，再在他所在的这一侧选点B，C，D，使得AB⊥BC，CD⊥BC，然后找出AD与BC的交点E．如图所示，若测得BE=90m，EC=45m，CD=60m，则这条河的宽AB等于（ ）
A、120m B、67.5m C、40m D、30m10. 小刚身高1.7m，测得他站立在阳光下的影子长为0.85m，紧接着他把手臂竖直举起，测得影子长为1.1m，那么小刚举起的手臂超出头顶（ ）A、0.5m B、0.55m C、0.6m D、2.2m二、填空题
-
11. 如图是小孔成像原理的示意图， ， ， . 若物体的高度为 ， 则像的高度是.
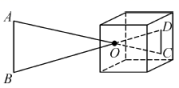12. 如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm．他准备了一支长为20cm的蜡烛，想要得到高度为5cm的像．蜡烛应放在距离纸筒 cm的地方．
13. 如图，道旁树在路灯O的照射下形成投影 ， 已知路灯O离地8m，树影长4m，树与路灯O的水平距离为6m，则树的高是m．
14. 如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为米．
15. 如图，放映幻灯时，通过光源，把幻灯片上的图形放大到屏幕上.若幻灯片到光源的距离为20 cm，到屏幕的距离为40 cm，且幻灯片中图形的高度为6 cm，则屏幕上图形的高度为cm.
三、解答题
-
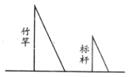
16. 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前．其中有首歌谣：今有竿不知其长，量得影长一丈五尺．立一标杆，长一尺五寸，影长五寸，问竿长几何?
意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸(提示：1丈=10尺，1尺=10寸)，求竹竿的长。
