2023-2024学年北师大版数学九年级上册4.5相似三角形判定定理的证明(培优卷)
试卷更新日期:2023-07-31 类型:同步测试
一、选择题
-
1. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )
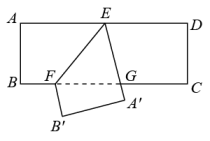 A、 B、 C、 D、2. 如图,在矩形中,点是边的三等分点 , 点是边的中点,线段 , 与对角线分别交于点 , .设矩形的面积为 , 则以下4个结论中:①;②;③;④.正确的结论有( )
A、 B、 C、 D、2. 如图,在矩形中,点是边的三等分点 , 点是边的中点,线段 , 与对角线分别交于点 , .设矩形的面积为 , 则以下4个结论中:①;②;③;④.正确的结论有( ) A、1个 B、2个 C、3个 D、4个3. 在正方形ABCD中,AB=3,点E在边CD上,且DE=1,将△ADE沿AE对折到△AFE,延长EF交边BC于点G,连接AG,CF.下列结论,其中正确的有( )个.
A、1个 B、2个 C、3个 D、4个3. 在正方形ABCD中,AB=3,点E在边CD上,且DE=1,将△ADE沿AE对折到△AFE,延长EF交边BC于点G,连接AG,CF.下列结论,其中正确的有( )个.

(1)CG=FG;(2)∠EAG=45°;(3)S△EFC=;(4)CF=GEA、1个 B、2个 C、3个 D、4个4. 如图,在正方形ABCD中,点E是边BC上一点,且 . 过点B作 , 交边CD于点F.以C为圆心,CF长为半径画圆,交边BC于点G,连接DG,交BF于点H.则( ) A、10:3 B、3:1 C、8:3 D、5:35. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.点P,Q分别为AB,GH的中点,若PQ恰好经过点F,则的值为( )
A、10:3 B、3:1 C、8:3 D、5:35. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.点P,Q分别为AB,GH的中点,若PQ恰好经过点F,则的值为( )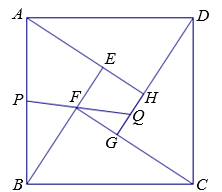 A、 B、3 C、 D、46. 如图,正方形中,E为的中点,于G,延长交于点F,延长交于点H,交于N下列结论:①;②;③;④;⑤;其中正确结论的个数有( )
A、 B、3 C、 D、46. 如图,正方形中,E为的中点,于G,延长交于点F,延长交于点H,交于N下列结论:①;②;③;④;⑤;其中正确结论的个数有( ) A、2个 B、3个 C、4个 D、5个7. 如图,已知菱形的边长为4,E是的中点,平分交于点F , 交于点G , 若 , 则的长是( )
A、2个 B、3个 C、4个 D、5个7. 如图,已知菱形的边长为4,E是的中点,平分交于点F , 交于点G , 若 , 则的长是( )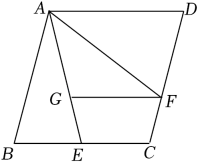 A、3 B、 C、 D、8. 如图,在正方形中,点是上一点,且 , 连接交对角线于点,过点作交的延长线于点 , 若 , 则的长为( )
A、3 B、 C、 D、8. 如图,在正方形中,点是上一点,且 , 连接交对角线于点,过点作交的延长线于点 , 若 , 则的长为( ) A、 B、 C、 D、9. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,过点作GD的垂线交AB于点 , 若 , 则的值为( )
A、 B、 C、 D、9. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,过点作GD的垂线交AB于点 , 若 , 则的值为( )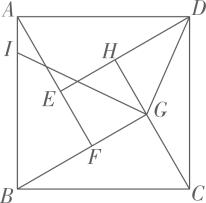 A、 B、 C、 D、10. 如图,在中, , , 点在上,过点作交于点 , 现将沿着所在的直线折叠,使得点落在点处, , 分别交于点、若:: , 则图中阴影部分的周长为( )
A、 B、 C、 D、10. 如图,在中, , , 点在上,过点作交于点 , 现将沿着所在的直线折叠,使得点落在点处, , 分别交于点、若:: , 则图中阴影部分的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,面积为4的正方形中,分别是各边的中点,将一边两端点分别和对边中点连结,所得阴影部分为各边相等的八边形,则八边形每条边的长度是.
 12. 如图,菱形ABCD的边长为4,∠BAD=60°,点E是边AB上一动点(不与点A、B重合),过点E作EF∥BC交AC于点F,连接DF,当△ADF是等腰三角形时,AE的长为.
12. 如图,菱形ABCD的边长为4,∠BAD=60°,点E是边AB上一动点(不与点A、B重合),过点E作EF∥BC交AC于点F,连接DF,当△ADF是等腰三角形时,AE的长为. 13. 如图,四边形ABCD是正方形,AB=6,E是BC的中点,连接DE,DE的垂直平分线分别交AB、DE、CD于点M、O、N,连接EN,过E作EF⊥EN交AB于点F,则AF的长为 .
13. 如图,四边形ABCD是正方形,AB=6,E是BC的中点,连接DE,DE的垂直平分线分别交AB、DE、CD于点M、O、N,连接EN,过E作EF⊥EN交AB于点F,则AF的长为 . 14. 如图,中, , , 点E为AC中点.点D在AC右侧, , 且 , 射线BE交AD于点F,若为等腰三角形,则线段EF的长为 .
14. 如图,中, , , 点E为AC中点.点D在AC右侧, , 且 , 射线BE交AD于点F,若为等腰三角形,则线段EF的长为 . 15. 图1是某个零件横截面的示意图,已知AB=CD,∠B=∠C,为了求出BC的长度,小艺将一根直尺按图2,图3,图4的三种方式摆放,所测得的具体数据(单位:cm)如图所示,则直尺宽为 cm,BC为 cm.
15. 图1是某个零件横截面的示意图,已知AB=CD,∠B=∠C,为了求出BC的长度,小艺将一根直尺按图2,图3,图4的三种方式摆放,所测得的具体数据(单位:cm)如图所示,则直尺宽为 cm,BC为 cm.
三、解答题
-
16. 如图(图形不全),等边三角形 中, ,点 在直线 上,点 在直线 上,且 ,当 时,求 的长.
几位同学通过探究得出结论:此题有多种结果.有同学已经得出两个符合题意结论:①当点 在边 上、点 在边 上时, ;②当点 在边 上、点 在 的延长线上时, .
要求:请针对其它情况,继续求出 的长,并写出总的正确结论.
 17. 如图, 是矩形 的边 上的一点, 于点 , , , .求 的长度.
17. 如图, 是矩形 的边 上的一点, 于点 , , , .求 的长度. 18. 如图,在 中,AB=AC,D、E、B、C在同一条直线上,且 .求证: ∽ .
18. 如图,在 中,AB=AC,D、E、B、C在同一条直线上,且 .求证: ∽ . 19. 在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
19. 在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.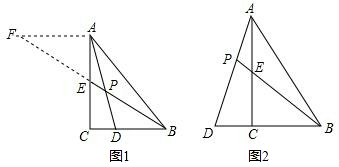
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,易得 的值为 ▲ .
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求 的值:
应用:若CD=2,AC=6,则BP= ▲ .
20. 如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.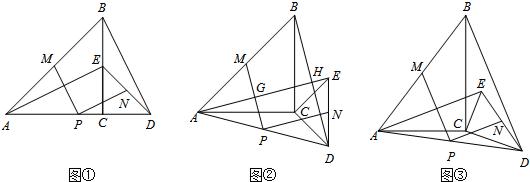 (1)、猜想PM与PN的数量关系及位置关系,请直接写出结论;(2)、现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)、若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
(1)、猜想PM与PN的数量关系及位置关系,请直接写出结论;(2)、现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)、若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.