2023-2024学年北师大版数学九年级上册4.4探索三角形相似的条件(培优卷)
试卷更新日期:2023-07-31 类型:同步测试
一、选择题
-
1. 如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F 在另一条直线上. 以下结论正确的是( )
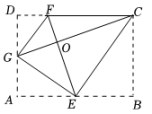 A、△COF∽△CEG B、OC=3OF C、AB:AD=4:3 D、GE=DF2. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A、△COF∽△CEG B、OC=3OF C、AB:AD=4:3 D、GE=DF2. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以点C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ) A、(6,5) B、(6,0) C、(6,4) D、(4,2)3. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )
A、(6,5) B、(6,0) C、(6,4) D、(4,2)3. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )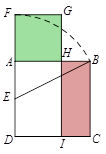 A、
A、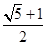 B、
B、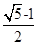 C、
D、1
4. 下列说法中正确的是( )A、两个直角三角形相似 B、两个等腰三角形相似 C、两个等边三角形相似 D、两个锐角三角形相似5. 在学习画线段的黄金分割点时,小明过点B作的垂线 , 取的中点M,以点B为圆心,为半径画弧交射线于点D,连接 , 再以点D为圆心,为半径画弧,前后所画的两弧分别与交于E,F两点,最后,以A为圆心,“■■”的长度为半径画弧交于点H,点H即为的其中一个黄金分割点,这里的“■■”指的是线段( )
C、
D、1
4. 下列说法中正确的是( )A、两个直角三角形相似 B、两个等腰三角形相似 C、两个等边三角形相似 D、两个锐角三角形相似5. 在学习画线段的黄金分割点时,小明过点B作的垂线 , 取的中点M,以点B为圆心,为半径画弧交射线于点D,连接 , 再以点D为圆心,为半径画弧,前后所画的两弧分别与交于E,F两点,最后,以A为圆心,“■■”的长度为半径画弧交于点H,点H即为的其中一个黄金分割点,这里的“■■”指的是线段( ) A、 B、 C、 D、6. 如图,在四边形中,与相交于点O,则下列三角形中,与一定相似的是( )
A、 B、 C、 D、6. 如图,在四边形中,与相交于点O,则下列三角形中,与一定相似的是( ) A、 B、 C、 D、7. 如图,在中,点Р在边上,则在下列四个条件中:①;②;③;④ , 能满足与相似的条件以及性质的是( )
A、 B、 C、 D、7. 如图,在中,点Р在边上,则在下列四个条件中:①;②;③;④ , 能满足与相似的条件以及性质的是( )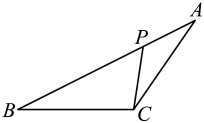 A、①②④ B、①③④ C、②③④ D、①②③8. 如图,点P在的边上,添加如下一个条件后,仍不能得到的是( )
A、①②④ B、①③④ C、②③④ D、①②③8. 如图,点P在的边上,添加如下一个条件后,仍不能得到的是( ) A、 B、 C、 D、9. 如图所示,网格中相似的两个三角形是( )
A、 B、 C、 D、9. 如图所示,网格中相似的两个三角形是( ) A、①与② B、①与③ C、③与④ D、②与③10. 已知在中, , 则下列选项中阴影部分的三角形与原不相似的是( )A、
A、①与② B、①与③ C、③与④ D、②与③10. 已知在中, , 则下列选项中阴影部分的三角形与原不相似的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如图,在中,点D,E分别为边 , 上的点,试添加一个条件: , 使得与相似.(任意写出一个满足条件的即可)
 12. 如图,要使 , 则需添加一个适当的条件是(添一个即可).
12. 如图,要使 , 则需添加一个适当的条件是(添一个即可). 13. 若线段AB=10,且点C是AB的黄金分割点,且BC>AC,则BC的长为 .14. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .15. 如图,在黄金矩形ABCD中,四边形ABFG、GHED均为正方形, ,现将矩形ABCD沿AE向上翻折,得四边形 ,连接BB′,若AB=2,则线段 的长度为.
13. 若线段AB=10,且点C是AB的黄金分割点,且BC>AC,则BC的长为 .14. 同学们学习了线段的黄金分割之后,曾老师提出了一个新的定义:点C是线段AB上一点,若=kn,则称点C为线段AB的“近A,n阶黄金分割点”.例如:若=k2 , 则称点C为线段AB的“近A,2阶黄金分割点”;若=k3 , 则称点C为线段AB的“近A,3阶黄金分割点”.若点C为线段AB的“近A,6阶黄金分割点”时,k6= .15. 如图,在黄金矩形ABCD中,四边形ABFG、GHED均为正方形, ,现将矩形ABCD沿AE向上翻折,得四边形 ,连接BB′,若AB=2,则线段 的长度为.
三、解答题
-
16. 如图,在中, , D是边上一点,.求证.
 17. 如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
17. 如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.


