2023-2024学年北师大版数学九年级上册4.4探索三角形相似的条件（基础卷）

试卷更新日期：2023-07-31 类型：同步测试

进入出卷网下载

一、选择题

1. 若点Р是线段 $A B$ 的黄金分割点 $(A P > P B)$ ， $A B = 2$ ，则 $A P$ 的长为（）

A、 $\sqrt{5} - 1$ B、 $3 - \sqrt{5}$ C、 $\sqrt{5} + 1$ D、 $3 + \sqrt{5}$

查看试题解析
2. 校园里一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄、金分割点(AP>PB)，如果AB的长度为10cm，那么AP的长度为（）cm．

A、 $\sqrt{5}$ -1 B、2 $\sqrt{5}$ -2 C、5 $\sqrt{5}$ -5 D、10 $\sqrt{5}$ -10

查看试题解析
3. 给出下列结论：
①任意两个等边三角形相似，②顶角对应相等的两个等腰三角形相似，③两条边对应成比例的两个直角三角形相似，其中正确的是（）

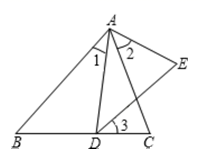
A、②③ B、①③ C、①② D、①②③

查看试题解析
4. 如图示，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，仍无法判定 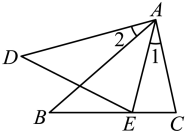$△ A B C ∽ △ A D E$ 的是（　　）

A、 $∠ D = ∠ B$ B、 $∠ C = ∠ A E D$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A B}{A D} = \frac{B C}{D E}$

查看试题解析
5. 如图，在△ABC中，点D、E分别在边AB、AC上，下列条件不能满足△ADE∽△ACB的条件是（）

A、∠AED=∠B B、 $\frac{A D}{A C} = \frac{A E}{A B}$ C、AD·BC= DE·AC D、DE//BC

查看试题解析
6. 如图，下列条件不能判定△ABC与△ADE相似的是（）

A、 $\frac{A E}{A D} = \frac{A C}{A B}$ B、∠B=∠ADE C、 $\frac{A E}{A C} = \frac{D E}{B C}$ D、∠C=∠AED

查看试题解析
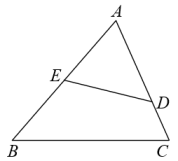
7. 已知图中有两组三角形，其边长和角的度数已在图上标注，对于各组中的两个三角形而言，下列说法正确的是（）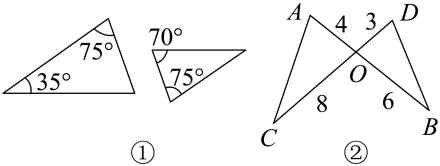

A、都相似 B、都不相似 C、只有①相似 D、只有②相似

查看试题解析
8. 在 $△ A B C$ 中，点D，E分别在边 $A B$ ， $A C$ 上，则在下列条件中，不能使得以A，D，E为顶点的三角形与 $△ A B C$ 相似的是（）

A、 $∠ A E D = ∠ B$ B、 $D E ∥ B C$ C、 $A D \cdot B C = D E \cdot A C$ D、 $∠ A D E = ∠ C$

查看试题解析
9. 如图，在△ABC中，点D，E分别是AB，AC上的点，连接DE，下列条件不能使得△ABC与△ADE相似的是（）

A、∠ADE＝∠ACB B、DE∥BC C、 $\frac{A E}{D E} = \frac{A B}{B C}$ D、 $\frac{A D}{A C} = \frac{A E}{A B}$

查看试题解析
10. 将一个三角形的各边都缩小到原来的 $\frac{1}{2}$ 后，得到三角形与原三角形（）

A、一定不相似 B、不一定相似 C、无法判断是否相似 D、一定相似

查看试题解析

二、填空题

11. 如果点 $P$ 是线段的黄金分割点， $A P < B P$ ，则 $A P ： B P =$ .

查看试题解析
12. 已知点C是线段AB的黄金分割点，且AC＞BC，若AB＝4，则BC的长为 .

查看试题解析
13. 在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果．如图，利用黄金分割法所作EF将矩形窗框ABCD分为上、下两部分，其中E为边AB的黄金分割点，即BE²=AE·AB，已知AB为2米，则线段BE的长为米(结果保留根号)．

查看试题解析
14. 已知点 $P$ 是线段 $A B$ 的黄金分割点，且 $A P > P B$ ，若 $A B = \sqrt{5} + 1$ ．则 $A P =$ ．

查看试题解析
15. 已知线段AB=10cm，点C是线段AB的黄金分割点，（AC>BC）则AC的长是．

查看试题解析

三、解答题

16. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ ， $F$ 分别在 $A B$ ， $B C$ ， $A C$ 边上， $D E ∥ A C$ ， $E F ∥ A B$ ．求证： $△ B D E ∼ △ E F C$

查看试题解析
17. 如图，在 $△ A B C$ 中，点D在 $A B$ 边上， $∠ A B C = ∠ A C D$ ，求证： $△ A B C ∽ △ A C D$ ．

查看试题解析
18. 如图，在△ABC中，BD平分∠ABC，交AC于点D，点E是AB上一点，连接DE，BD²=BC·BE.
证明：△BCD∽△BDE.

查看试题解析
19. 如图， $B E$ 是 $△ A B C$ 的角平分线，延长 $B E$ 至点 $D ，$ 使得 $B C = C D$ .求证： $△ A B E \sim △ C D E$ .

查看试题解析
20. 如图，已知 $∠ 1 = ∠ 2 = ∠ 3$ ，则 $Δ A B C 与 Δ A D E$ 相似吗？说明理由。

查看试题解析