2023年湖南省中考数学真题分类汇编:四边形、命题与证明
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 下列命题正确的是( )A、正方形的对角线相等且互相平分 B、对角互补的四边形是平行四边形 C、矩形的对角线互相垂直 D、一组邻边相等的四边形是菱形2. 如图所示,在矩形中, , 与相交于点O,下列说法正确的是( )
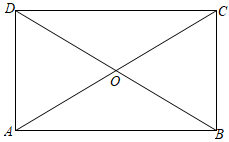 A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴3. 一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知 , 点D为边的中点,点A、B对应的刻度为1、7,则( )
A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴3. 一技术人员用刻度尺(单位:)测量某三角形部件的尺寸.如图所示,已知 , 点D为边的中点,点A、B对应的刻度为1、7,则( ) A、 B、 C、 D、4. 下列命题是真命题的是( )A、同位角相等 B、菱形的四条边相等 C、正五边形是中心对称图形 D、单项式的次数是45. 我们可以用以下推理来证明“在一个三角形中,至少有一个内角小于或等于”.假设三角形没有一个内角小于或等于 , 即三个内角都大于 . 则三角形的三个内角的和大于 , 这与“三角形的内角和等于”这个定理矛盾.所以在一个三角形中,至少有一个内角小于或等于 . 上述推理使用的证明方法是( )A、反证法 B、比较法 C、综合法 D、分析法6. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )
A、 B、 C、 D、4. 下列命题是真命题的是( )A、同位角相等 B、菱形的四条边相等 C、正五边形是中心对称图形 D、单项式的次数是45. 我们可以用以下推理来证明“在一个三角形中,至少有一个内角小于或等于”.假设三角形没有一个内角小于或等于 , 即三个内角都大于 . 则三角形的三个内角的和大于 , 这与“三角形的内角和等于”这个定理矛盾.所以在一个三角形中,至少有一个内角小于或等于 . 上述推理使用的证明方法是( )A、反证法 B、比较法 C、综合法 D、分析法6. 如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( ) A、AB=CD B、AB∥CD C、∠A=∠C D、BC=AD
A、AB=CD B、AB∥CD C、∠A=∠C D、BC=AD二、填空题
-
7. 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是 个.
 8. 如图,在平面直角坐标系中,四边形是正方形,点的坐标为 , 是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点 , , , 为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是 .
8. 如图,在平面直角坐标系中,四边形是正方形,点的坐标为 , 是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点 , , , 为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是 .
三、综合题
-
9. 如图所示,在平面直角坐标系中,四边形为正方形,其中点A、C分别在x轴负半轴,y轴负半轴上,点B在第三象限内,点 , 点在函数的图像上
 (1)、求k的值;(2)、连接 , 记的面积为S,设 , 求T的最大值.10. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.
(1)、求k的值;(2)、连接 , 记的面积为S,设 , 求T的最大值.10. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.①求函数的图像的对称轴;
②函数的图像是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由;
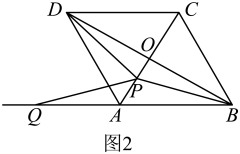
(3)、在同一平面直角坐标系中,若关于x的二次函数与它的“美美与共”函数的图像顶点分别为点A,点B,函数的图像与x轴交于不同两点C,D,函数的图像与x轴交于不同两点E,F.当时,以A,B,C,D为顶点的四边形能否为正方形?若能,求出该正方形面积的取值范围;若不请说明理由.11. 如图,在平面直角坐标系中,已知二次函数的图象与x轴交于点和点两点,与y轴交于点 . 点D为线段上的一动点. (1)、求二次函数的表达式;(2)、如图1,求周长的最小值;(3)、如图2,过动点D作交抛物线第一象限部分于点P,连接 , 记与的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.12.(1)、[问题探究]
(1)、求二次函数的表达式;(2)、如图1,求周长的最小值;(3)、如图2,过动点D作交抛物线第一象限部分于点P,连接 , 记与的面积和为S,当S取得最大值时,求点P的坐标,并求出此时S的最大值.12.(1)、[问题探究]如图1,在正方形中,对角线相交于点O.在线段上任取一点P(端点除外),连接 .
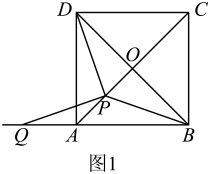
①求证:;
②将线段绕点P逆时针旋转,使点D落在的延长线上的点Q处.当点P在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系,并说明理由.
(2)、[迁移探究]如图2,将正方形换成菱形 , 且 , 其他条件不变.试探究与的数量关系,并说明理由.