2023年湖南省中考数学真题分类汇编:三角形
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 下列长度的各组线段能组成一个三角形的是( )A、 B、 C、 D、2. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,63. “莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边的边长为3,则该“莱洛三角形”的周长等于( )
 A、 B、 C、 D、4. 下列说法错误的是( )A、成语“水中捞月”表示的事件是不可能事件 B、一元二次方程有两个相等的实数根 C、任意多边形的外角和等于 D、三角形三条中线的交点叫作三角形的重心5. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、 B、 C、 D、4. 下列说法错误的是( )A、成语“水中捞月”表示的事件是不可能事件 B、一元二次方程有两个相等的实数根 C、任意多边形的外角和等于 D、三角形三条中线的交点叫作三角形的重心5. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )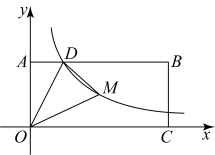 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
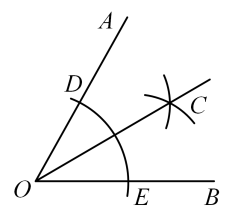
6. 如图,①在上分别截取线段 , 使;②分别以为圆心,以大于的长为半径画弧,在内两弧交于点;③作射线 . 若 , 则 .
 7. 如图,已知 , 点D在上,以点B为圆心,长为半径画弧,交于点E,连接 , 则的度数是 度.
7. 如图,已知 , 点D在上,以点B为圆心,长为半径画弧,交于点E,连接 , 则的度数是 度. 8. 如图,为的平分线,且 , 将四边形绕点逆时针方向旋转后,得到四边形 , 且 , 则四边形旋转的角度是 .
8. 如图,为的平分线,且 , 将四边形绕点逆时针方向旋转后,得到四边形 , 且 , 则四边形旋转的角度是 . 9. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数)
9. 沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”,如图.是以O为圆心,为半径的圆弧,C是弦的中点,D在上, . “会圆术”给出长l的近似值s计算公式: , 当 , 时, . (结果保留一位小数) 10. 如图,在中, , , . 将绕点逆时针旋转,得到 , 若点的对应点恰好落在线段上,则点的运动路径长是cm(结果用含的式子表示).
10. 如图,在中, , , . 将绕点逆时针旋转,得到 , 若点的对应点恰好落在线段上,则点的运动路径长是cm(结果用含的式子表示). 11. 《周礼考工记》中记载有:“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”意思是:“……直角的一半的角叫做宣,一宣半的角叫做欘……”.即:1宣矩,1欘宣(其中,1矩),问题:图(1)为中国古代一种强弩图,图(2)为这种强弩图的部分组件的示意图,若矩,欘,则度.
11. 《周礼考工记》中记载有:“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”意思是:“……直角的一半的角叫做宣,一宣半的角叫做欘……”.即:1宣矩,1欘宣(其中,1矩),问题:图(1)为中国古代一种强弩图,图(2)为这种强弩图的部分组件的示意图,若矩,欘,则度.

 12. 如图,在中, . 以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为 .
12. 如图,在中, . 以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为 . 13. 如图,在矩形中, , 动点在矩形的边上沿运动.当点不与点重合时,将沿对折,得到 , 连接 , 则在点的运动过程中,线段的最小值为 .
13. 如图,在矩形中, , 动点在矩形的边上沿运动.当点不与点重合时,将沿对折,得到 , 连接 , 则在点的运动过程中,线段的最小值为 .
三、作图题
-
14. 如图,四边形是平行四边形.
 (1)、尺规作图;作对角线的垂直平分线(保留作图痕迹);(2)、若直线分别交 , 于 , 两点,求证:四边形是菱形
(1)、尺规作图;作对角线的垂直平分线(保留作图痕迹);(2)、若直线分别交 , 于 , 两点,求证:四边形是菱形四、综合题
-
15. 年月日点分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是 , 仰角为;后飞船到达处,此时测得仰角为 .
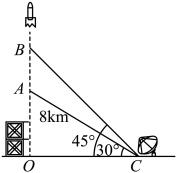 (1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)16. 如图, , , , 垂足分别为 , .
(1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)16. 如图, , , , 垂足分别为 , .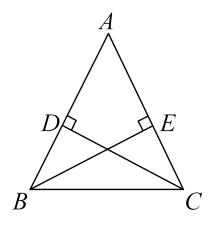 (1)、求证:;(2)、若 , , 求的长.17. 如图,二次函数的图象与x轴交于 , 两点,与y轴交于点C,顶点为D.O为坐标原点, .
(1)、求证:;(2)、若 , , 求的长.17. 如图,二次函数的图象与x轴交于 , 两点,与y轴交于点C,顶点为D.O为坐标原点, .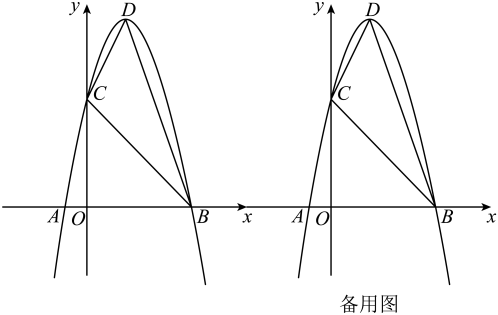 (1)、求二次函数的表达式;(2)、求四边形的面积;(3)、P是抛物线上的一点,且在第一象限内,若 , 求P点的坐标.18. 如图所示,在中,点D、E分别为的中点,点H在线段上,连接 , 点G、F分别为的中点.
(1)、求二次函数的表达式;(2)、求四边形的面积;(3)、P是抛物线上的一点,且在第一象限内,若 , 求P点的坐标.18. 如图所示,在中,点D、E分别为的中点,点H在线段上,连接 , 点G、F分别为的中点. (1)、求证:四边形为平行四边形(2)、 , 求线段的长度.19. 如图,点在的边上, , 请从以下三个选项中①;②;③ , 选择一个合适的选项作为已知条件,使为矩形.
(1)、求证:四边形为平行四边形(2)、 , 求线段的长度.19. 如图,点在的边上, , 请从以下三个选项中①;②;③ , 选择一个合适的选项作为已知条件,使为矩形.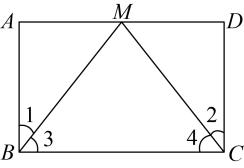 (1)、你添加的条件是(填序号);(2)、添加条件后,请证明为矩形.20. 如图,矩形中,过对角线的中点作的垂线 , 分别交 , 于点 , .
(1)、你添加的条件是(填序号);(2)、添加条件后,请证明为矩形.20. 如图,矩形中,过对角线的中点作的垂线 , 分别交 , 于点 , .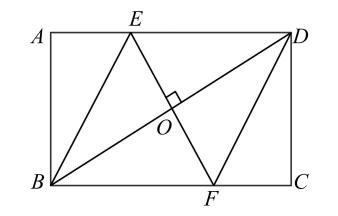 (1)、证明:;(2)、连接、 , 证明:四边形是菱形.21. 已知是等边三角形,点是射线上的一个动点,延长至点 , 使 , 连接交射线于点 .
(1)、证明:;(2)、连接、 , 证明:四边形是菱形.21. 已知是等边三角形,点是射线上的一个动点,延长至点 , 使 , 连接交射线于点 .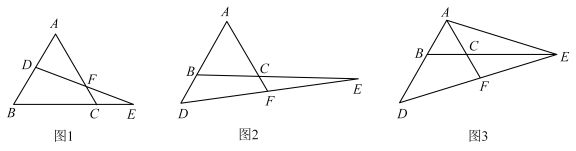 (1)、如图1,当点在线段上时,猜测线段与的数量关系并说明理由;(2)、如图2,当点在线段的延长线上时,
(1)、如图1,当点在线段上时,猜测线段与的数量关系并说明理由;(2)、如图2,当点在线段的延长线上时,①线段与的数量关系是否仍然成立?请说明理由;
②如图3,连接 . 设 , 若 , 求四边形的面积.
22. 如图,在平面直角坐标系中,抛物线经过点和点 , 且与直线交于两点(点在点的右侧),点为直线上的一动点,设点的横坐标为 . (1)、求抛物线的解析式.(2)、过点作轴的垂线,与拋物线交于点 . 若 , 求面积的最大值.(3)、抛物线与轴交于点 , 点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.23. 如图1,在中, , 点分别为边的中点,连接 .
(1)、求抛物线的解析式.(2)、过点作轴的垂线,与拋物线交于点 . 若 , 求面积的最大值.(3)、抛物线与轴交于点 , 点为平面直角坐标系上一点,若以为顶点的四边形是菱形,请求出所有满足条件的点的坐标.23. 如图1,在中, , 点分别为边的中点,连接 . (1)、初步尝试:与的数量关系是 , 与的位置关系是 .(2)、特例研讨:如图2,若 , 先将绕点顺时针旋转(为锐角),得到 , 当点在同一直线上时,与相交于点 , 连接 .
(1)、初步尝试:与的数量关系是 , 与的位置关系是 .(2)、特例研讨:如图2,若 , 先将绕点顺时针旋转(为锐角),得到 , 当点在同一直线上时,与相交于点 , 连接 .①求的度数;
②求的长.
(3)、深入探究:若 , 将绕点顺时针旋转 , 得到 , 连接 , . 当旋转角满足 , 点在同一直线上时,利用所提供的备用图探究与的数量关系,并说明理由.24. 如图,已知抛物线与x轴交于点和点B,与y轴交于点C,连接 , 过B、C两点作直线. (1)、求a的值.(2)、将直线向下平移个单位长度,交抛物线于、两点.在直线上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线的距离最大,若存在,请求出点D的坐标;若不存在,请说明理由.(3)、抛物线上是否存在点P,使 , 若存在,请求出直线的解析式;若不存在,请说明理由.
(1)、求a的值.(2)、将直线向下平移个单位长度,交抛物线于、两点.在直线上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线的距离最大,若存在,请求出点D的坐标;若不存在,请说明理由.(3)、抛物线上是否存在点P,使 , 若存在,请求出直线的解析式;若不存在,请说明理由.
-