2023年湖南省中考数学真题分类汇编:相交线与平行线
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
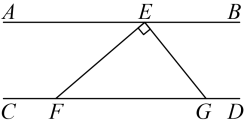
1. 已知 , 点在直线上,点在直线上,于点 , 则的度数是( )
 A、 B、 C、 D、2. 如图,平移直线至 , 直线 , 被直线所截, , 则的度数为( )
A、 B、 C、 D、2. 如图,平移直线至 , 直线 , 被直线所截, , 则的度数为( )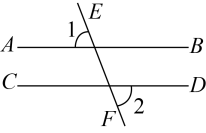 A、 B、 C、 D、3. 如图,直线直线n,点A在直线n上,点B在直线m上,连接 , 过点A作 , 交直线m于点C.若 , 则的度数为( )
A、 B、 C、 D、3. 如图,直线直线n,点A在直线n上,点B在直线m上,连接 , 过点A作 , 交直线m于点C.若 , 则的度数为( )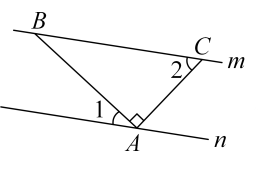 A、 B、 C、 D、4. 如图,已知直线 , 平分 , , 则的度数是( )
A、 B、 C、 D、4. 如图,已知直线 , 平分 , , 则的度数是( )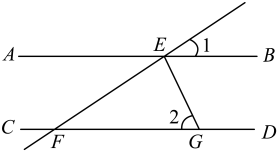 A、 B、 C、 D、5. 如图1,在正方形中,对角线相交于点O,E,F分别为 , 上的一点,且 , 连接 . 若 , 则的度数为( )
A、 B、 C、 D、5. 如图1,在正方形中,对角线相交于点O,E,F分别为 , 上的一点,且 , 连接 . 若 , 则的度数为( )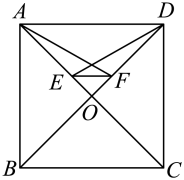 A、 B、 C、 D、6. 如图,在四边形中, , 若添加一个条件,使四边形为平形四边形,则下列正确的是( )
A、 B、 C、 D、6. 如图,在四边形中, , 若添加一个条件,使四边形为平形四边形,则下列正确的是( )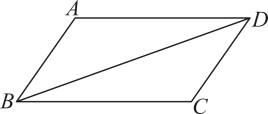 A、 B、 C、 D、7. 如图,直线被直线所截,已知 , 则的大小为( )
A、 B、 C、 D、7. 如图,直线被直线所截,已知 , 则的大小为( )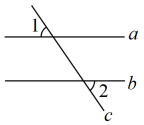 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 如图1,在中, , , , D是上一点,且 , 过点D作交于E,将绕A点顺时针旋转到图2的位置.则图2中的值为 .
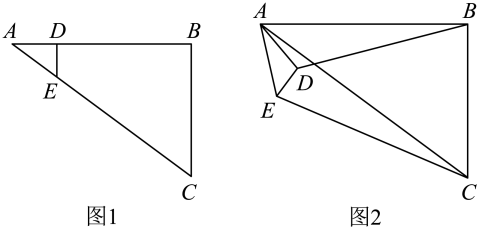 9. 如图,在平行四边形中, , , 的平分线交于点E,则的长为 .
9. 如图,在平行四边形中, , , 的平分线交于点E,则的长为 .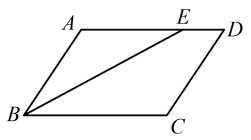 10. 如图,点是正方形的对角线上的一点,于点 , . 则点到直线的距离为 .
10. 如图,点是正方形的对角线上的一点,于点 , . 则点到直线的距离为 .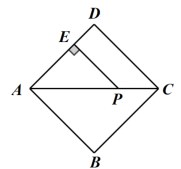
三、解答题
-
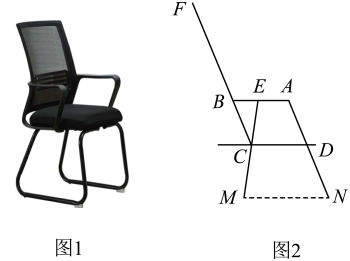
11. 今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且 , , 靠背 , 支架 , 扶手的一部分 . 这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据: , , )
四、综合题
-
12. 如图,在中,平分 , 交于点E,交的延长线于点F.
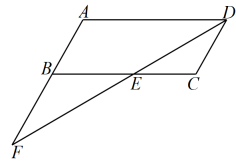 (1)、求证:;(2)、若 , 求的长和的面积.13. 如图,已知点A,D,C,B在同一条直线上,且 , , .
(1)、求证:;(2)、若 , 求的长和的面积.13. 如图,已知点A,D,C,B在同一条直线上,且 , , .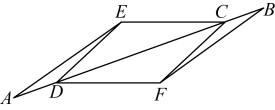 (1)、求证:;(2)、若时,求证:四边形是菱形.14. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点 .
(1)、求证:;(2)、若时,求证:四边形是菱形.14. 如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点 .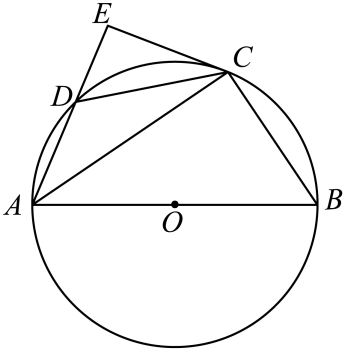 (1)、求证:是的切线;(2)、若 , , 求的长.15. 如图, , 点是线段上的一点,且 . 已知 .
(1)、求证:是的切线;(2)、若 , , 求的长.15. 如图, , 点是线段上的一点,且 . 已知 .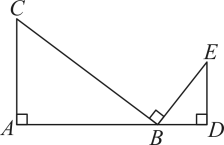 (1)、证明: .(2)、求线段的长.16. 如图所示,在某交叉路口,一货车在道路①上点A处等候“绿灯”一辆车从被山峰遮挡的道路②上的点B处由南向北行驶.已知 , , 线段的延长线交直线于点D.
(1)、证明: .(2)、求线段的长.16. 如图所示,在某交叉路口,一货车在道路①上点A处等候“绿灯”一辆车从被山峰遮挡的道路②上的点B处由南向北行驶.已知 , , 线段的延长线交直线于点D.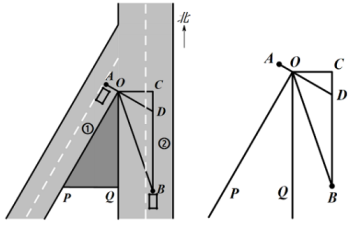 (1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)
(1)、求的大小;(2)、若在点B处测得点O在北偏西方向上,其中米.问该轿车至少行驶多少米才能发现点A处的货车?(当该轿车行驶至点D处时,正好发现点A处的货车)
-