2023年湖南省中考数学真题分类汇编：一次函数、二次函数

试卷更新日期：2023-07-30 类型：二轮复习

进入出卷网下载

一、选择题

1. 下列一次函数中，y随x的增大而减小的函数是（　　）

A、 $y = 2 x + 1$ B、 $y = x - 4$ C、 $y = 2 x$ D、 $y = - x + 1$

查看试题解析
2. 已知 $P_{1} (x_{1} ， y_{1}) ， P_{2} (x_{2} ， y_{2})$ 是抛物线 $y = a x^{2} + 4 a x + 3$ （a是常数， $a \neq 0)$ 上的点，现有以下四个结论：①该抛物线的对称轴是直线 $x = - 2$ ；②点 $(0 ， 3)$ 在抛物线上；③若 $x_{1} > x_{2} > - 2$ ，则 $y_{1} > y_{2}$ ；④若 $y_{1} = y_{2}$ ，则 $x_{1} + x_{2} = - 2$ 其中，正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图所示，直线l为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像的对称轴，则下列说法正确的是（）

A、b恒大于0 B、a，b同号 C、a，b异号 D、以上说法都不对

查看试题解析
4. 已知 $m > n > 0$ ，若关于x的方程 $x^{2} + 2 x - 3 - m = 0$ 的解为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ．关于x的方程 $x^{2} + 2 x - 3 - n = 0$ 的解为 $x_{3} ， x_{4} (x_{3} < x_{4})$ ．则下列结论正确的是（）

A、 $x_{3} < x_{1} < x_{2} < x_{4}$ B、 $x_{1} < x_{3} < x_{4} < x_{2}$ C、 $x_{1} < x_{2} < x_{3} < x_{4}$ D、 $x_{3} < x_{4} < x_{1} < x_{2}$

查看试题解析

二、填空题

5. 在一次函数 $y = (k - 2) x + 3$ 中， $y$ 随 $x$ 的增大而增大，则 $k$ 的值可以是（任写一个符合条件的数即可）．

查看试题解析
6. 抛物线 $y = x^{2} - 6 x + c$ 与 $x$ 轴只有一个交点，则 $c =$ ．

查看试题解析

三、综合题

7. 如图，二次函数的图象与x轴交于 $A (- 1 ， 0)$ ， $B (5 ， 0)$ 两点，与y轴交于点C，顶点为D．O为坐标原点， $t a n ∠ A C O = \frac{1}{5}$ ．

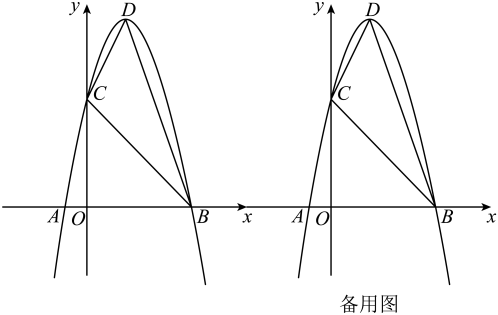(1)、求二次函数的表达式；

(2)、求四边形 $A C D B$ 的面积；

(3)、P是抛物线上的一点，且在第一象限内，若 $∠ A C O = ∠ P B C$ ，求P点的坐标．

查看试题解析
8. 某花店每天购进 $16$ 支某种花，然后出售．如果当天售不完，那么剩下的这种花进行作废处理、该花店记录了 $10$ 天该种花的日需求量n（n为正整数，单位：支），统计如下表：
日需求量n
          $13$
          $14$
          $15$
          $16$
          $17$
          $18$
天数
1
1
2
4
1
1

(1)、求该花店在这 $10$ 天中出现该种花作废处理情形的天数；

(2)、当 $n < 16$ 时，日利润y（单位：元）关于n的函数表达式为： $y = 10 n - 80$ ；当 $n \geq 16$ 时，日利润为 $80$ 元．
①当 $n = 14$ 时，间该花店这天的利润为多少元？
②求该花店这 $10$ 天中日利润为 $70$ 元的日需求量的频率．

查看试题解析
9. 如图，在平面直角坐标系中，已知二次函数 $y = a x^{2} + b x + c$ 的图象与x轴交于点 $A (- 2 ， 0)$ 和点 $B (6 ， 0)$ 两点，与y轴交于点 $C (0 ， 6)$ ．点D为线段 $B C$ 上的一动点．

(1)、求二次函数的表达式；

(2)、如图1，求 $△ A O D$ 周长的最小值；

(3)、如图2，过动点D作 $D P ∥ A C$ 交抛物线第一象限部分于点P，连接 $P A ， P B$ ，记 $△ P A D$ 与 $△ P B D$ 的面积和为S，当S取得最大值时，求点P的坐标，并求出此时S的最大值．

查看试题解析
10. 已知抛物线 $y = a x^{2} + b x + 4$ 与 $x$ 轴相交于点 $A (1 ， 0)$ ， $B (4 ， 0)$ ，与 $y$ 轴相交于点 $C$ ．

(1)、求抛物线的表达式；

(2)、如图1，点 $P$ 是抛物线的对称轴 $l$ 上的一个动点，当 $△ P A C$ 的周长最小时，求 $\frac{P A}{P C}$ 的值；

(3)、如图2，取线段 $O C$ 的中点 $D$ ，在抛物线上是否存在点 $Q$ ，使 $t a n ∠ Q D B = \frac{1}{2}$ ？若存在，求出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析
11. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + x + c$ 经过点 $A (- 2 ， 0)$ 和点 $B (4 ， 0)$ ，且与直线 $l ： y = - x - 1$ 交于 $D 、 E$ 两点（点 $D$ 在点 $E$ 的右侧），点 $M$ 为直线 $l$ 上的一动点，设点 $M$ 的横坐标为 $t$ ．

(1)、求抛物线的解析式．

(2)、过点 $M$ 作 $x$ 轴的垂线，与拋物线交于点 $N$ ．若 $0 < t < 4$ ，求 $△ N E D$ 面积的最大值．

(3)、抛物线与 $y$ 轴交于点 $C$ ，点 $R$ 为平面直角坐标系上一点，若以 $B 、 C 、 M 、 R$ 为顶点的四边形是菱形，请求出所有满足条件的点 $R$ 的坐标．

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c (a > 0)$ ．

(1)、若 $a = 1 ， c = - 1$ ，且该二次函数的图象过点 $(2 ， 0)$ ，求 $b$ 的值；

(2)、如图所示，在平面直角坐标系 $O x y$ 中，该二次函数的图象与 $x$ 轴交于点 $A (x_{1} ， 0) ， B (x_{2} ， 0)$ ，且 $x_{1} < 0 < x_{2}$ ，点D在 $⊙ O$ 上且在第二象限内，点 $E$ 在 $x$ 轴正半轴上，连接 $D E$ ，且线段 $D E$ 交 $y$ 轴正半轴于点 $F$ ， $∠ D O F = ∠ D E O ， O F = \frac{3}{2} D F$ ．

①求证： $\frac{D O}{E O} = \frac{2}{3}$ ．
②当点 $E$ 在线段 $O B$ 上，且 $B E = 1$ ． $⊙ O$ 的半径长为线段 $O A$ 的长度的 $2$ 倍，若 $4 a c = - a^{2} - b^{2}$ ，求 $2 a + b$ 的值．

查看试题解析
13. 已知抛物线 $Q_{1} ： y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A (- 3 ， 0) ， B$ 两点，交 $y$ 轴于点 $C (0 ， 3)$ ．

(1)、请求出抛物线 $Q_{1}$ 的表达式．

(2)、如图1，在 $y$ 轴上有一点 $D (0 ， - 1)$ ，点 $E$ 在抛物线 $Q_{1}$ 上，点 $F$ 为坐标平面内一点，是否存在点 $E ， F$ 使得四边形 $D A E F$ 为正方形？若存在，请求出点 $E ， F$ 的坐标；若不存在，请说明理由．

(3)、如图2，将抛物线 $Q_{1}$ 向右平移2个单位，得到抛物线 $Q_{2}$ ，抛物线 $Q_{2}$ 的顶点为 $K$ ，与 $x$ 轴正半轴交于点 $H$ ，抛物线 $Q_{1}$ 上是否存在点 $P$ ，使得 $∠ C P K = ∠ C H K$ ？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析
14. 如图，已知抛物线 $y = a x^{2} - 2 a x + 3$ 与x轴交于点 $A (- 1 ， 0)$ 和点B，与y轴交于点C，连接 $A C$ ，过B、C两点作直线．

(1)、求a的值．

(2)、将直线 $B C$ 向下平移 $m (m > 0)$ 个单位长度，交抛物线于 $B^{'}$ 、 $C^{'}$ 两点．在直线 $B^{^{'}} C^{^{'}}$ 上方的抛物线上是否存在定点D，无论m取何值时，都是点D到直线 $B^{^{'}} C^{^{'}}$ 的距离最大，若存在，请求出点D的坐标；若不存在，请说明理由．

(3)、抛物线上是否存在点P，使 $∠ P B C + ∠ A C O = 45 °$ ，若存在，请求出直线 $B P$ 的解析式；若不存在，请说明理由．

查看试题解析
15. 如图一所示，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 8$ 与 $x$ 轴交于 $A (- 4 ， 0) 、 B (2 ， 0)$ 两点，与 $y$ 轴交于点 $C$ ．

(1)、求抛物线的函数表达式及顶点坐标；

(2)、点 $P$ 为第三象限内抛物线上一点，作直线 $A C$ ，连接 $P A$ 、 $P C$ ，求 $△ P A C$ 面积的最大值及此时点 $P$ 的坐标；

(3)、设直线 $l_{1} ： y = k x + k - \frac{35}{4}$ 交抛物线于点 $M$ 、 $N$ ，求证：无论 $k$ 为何值，平行于 $x$ 轴的直线 $l_{2} ： y = - \frac{37}{4}$ 上总存在一点 $E$ ，使得 $∠ M E N$ 为直角．

查看试题解析

日需求量n	$13$	$14$	$15$	$16$	$17$	$18$
天数	1	1	2	4	1	1