2023年湖南省中考数学真题分类汇编:平面直角坐标系、反比例函数
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 已知压力、压强与受力面积之间有如下关系式: . 当F为定值时,下图中大致表示压强p与受力面积S之间函数关系的是( )A、
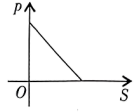 B、
B、 C、
C、 D、
D、 2. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为 , 则点的坐标为( )
2. 如图,矩形的顶点和正方形的顶点都在反比例函数的图像上,点的坐标为 , 则点的坐标为( ) A、 B、 C、 D、3. 下列哪个点在反比例函数的图像上?( )A、 B、 C、 D、4. 如图,反比例函数的图象与过点的直线相交于、两点.已知点的坐标为 , 点为轴上任意一点.如果 , 那么点的坐标为( )
A、 B、 C、 D、3. 下列哪个点在反比例函数的图像上?( )A、 B、 C、 D、4. 如图,反比例函数的图象与过点的直线相交于、两点.已知点的坐标为 , 点为轴上任意一点.如果 , 那么点的坐标为( ) A、 B、 C、或 D、或5. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、 B、 C、或 D、或5. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )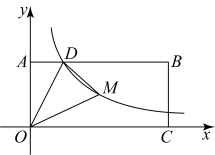 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
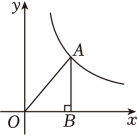
6. 在平面直角坐标系中,点所在象限是第象限.7. 如图,在平面直角坐标系中,点在反比例函数为常数, , 的图象上,过点作轴的垂线,垂足为 , 连接 . 若的面积为 , 则 .
三、综合题
-
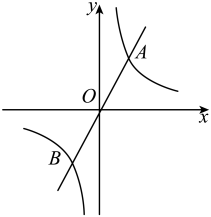
8. 如图所示,一次函数与反比例函数相交于点A和点 .
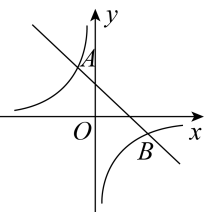 (1)、求m的值和反比例函数解析式;(2)、当时,求x的取值范围.9. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
(1)、求m的值和反比例函数解析式;(2)、当时,求x的取值范围.9. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
托盘与点的距离
30
25
20
15
10
容器与水的总质量
10
12
15
20
30
加入的水的质量
5
7
10
15
25
把上表中的与各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的关于的函数图象.
 (1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:
(1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:①猜测与之间的函数关系,并求关于的函数表达式;
②求关于的函数表达式;
③当时,随的增大而(填“增大”或“减小”),随的增大而(填“增大”或“减小”),的图象可以由的图象向(以“上”或“下”或“左”或“右”)平移得到.
(3)、若在容器中加入的水的质量(g)满足 , 求托盘与点的距离(cm)的取值范围.10. 如图所示,在平面直角坐标系中,四边形为正方形,其中点A、C分别在x轴负半轴,y轴负半轴上,点B在第三象限内,点 , 点在函数的图像上 (1)、求k的值;(2)、连接 , 记的面积为S,设 , 求T的最大值.
(1)、求k的值;(2)、连接 , 记的面积为S,设 , 求T的最大值.