2023年四川省中考数学真题分类汇编:锐角三角函数、投影与视图
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是( )
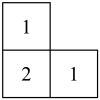 A、
A、 B、
B、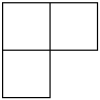 C、
C、 D、
D、 2. 一个立体图形的三视图如图所示,则该立体图形是( )
2. 一个立体图形的三视图如图所示,则该立体图形是( )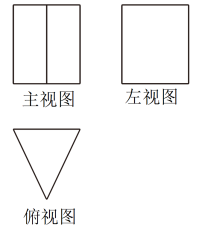 A、圆柱 B、圆锥 C、长方体 D、三棱柱3. 如图是由5个完全相同的小正方体堆成的物体,其主视图是( )
A、圆柱 B、圆锥 C、长方体 D、三棱柱3. 如图是由5个完全相同的小正方体堆成的物体,其主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,由5个大小相同的小正方体搭成的几何体,它的俯视图是( )
4. 如图,由5个大小相同的小正方体搭成的几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
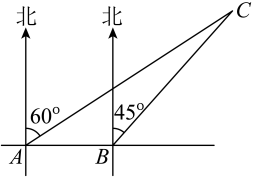
D、 5. 如图,小兵同学从处出发向正东方向走米到达处,再向正北方向走到处,已知 , 则 , 两处相距( )
5. 如图,小兵同学从处出发向正东方向走米到达处,再向正北方向走到处,已知 , 则 , 两处相距( ) A、米 B、米 C、米 D、米6. 由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )
A、米 B、米 C、米 D、米6. 由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为( )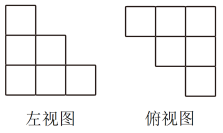 A、6 B、9 C、10 D、147. 生活中一些常见的物体可以抽象成立体图形,以下立体图形中三视图形状相同的可能是( )
A、6 B、9 C、10 D、147. 生活中一些常见的物体可以抽象成立体图形,以下立体图形中三视图形状相同的可能是( )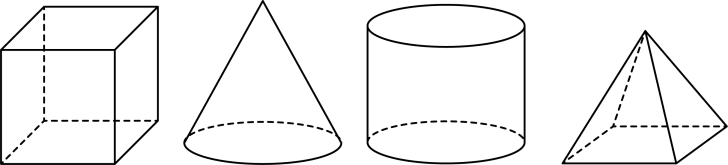 A、正方体 B、圆锥 C、圆柱 D、四棱锥8. 如图是由4个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
A、正方体 B、圆锥 C、圆柱 D、四棱锥8. 如图是由4个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图中六棱柱的左视图是( )
9. 如图中六棱柱的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
10. 一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是海里.
 11. 一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有个.
11. 一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有个.
三、解答题
-
12. 某实践探究小组想测得湖边两处的距离,数据勘测组通过勘测,得到了如下记录表:
实践探究活动记录表
活动内容 测量湖边A、B两处的距离
成员 组长:××× 组员:××××××××××××
测量工具 测角仪,皮尺等
测量示意图

说明:因为湖边A、B两处的距离无法直接测量,数据勘测组在湖边找了一处位置C.可测量C处到A、B两处的距离.通过测角仪可测得的度数.
测量数据
角的度数
边的长度
米
米
数据处理组得到上面数据以后做了认真分析.他们发现不需要勘测组的全部数据就可以计算出A、B之间的距离.于是数据处理组写出了以下过程,请补全内容.
(1)、已知:如图,在中, . ____.(从记录表中再选一个条件填入横线)

求:线段的长.(为减小结果的误差,若有需要,取 , 取 , 取进行计算,最后结果保留整数.)
13. 渝昆高速铁路的建成,将会显著提升宜宾的交通地位.渝昆高速铁路宜宾临港长江公铁两用大桥(如图),桥面采用国内首创的公铁平层设计.为测量左桥墩底到桥面的距离 , 如图 . 在桥面上点处,测得到左桥墩的距离米,左桥墩所在塔顶的仰角 , 左桥墩底的俯角 , 求的长度.(结果精确到米.参考数据: , ) 14. 为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,便于社区居民休憩.
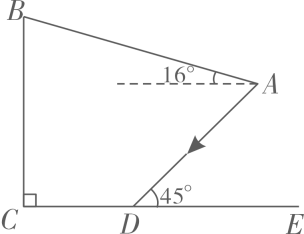
14. 为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,便于社区居民休憩.如图,在侧面示意图中,遮阳篷AB长为5米,与水平面的夹角为16°,且靠墙端离地高BC为4米,当太阳光线AD与地面CE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据: , , )

 15. 如图,某数学兴趣小组为了测量古树的高度,采用了如下的方法:先从与古树底端在同一水平线上的点A出发,沿斜面坡度为的斜坡前进到达点 , 再沿水平方向继续前进一段距离后到达点 . 在点处测得古树的顶端的俯角为 , 底部的俯角为 , 求古树的高度(参考数据: , , , 计算结果用根号表示,不取近似值).
15. 如图,某数学兴趣小组为了测量古树的高度,采用了如下的方法:先从与古树底端在同一水平线上的点A出发,沿斜面坡度为的斜坡前进到达点 , 再沿水平方向继续前进一段距离后到达点 . 在点处测得古树的顶端的俯角为 , 底部的俯角为 , 求古树的高度(参考数据: , , , 计算结果用根号表示,不取近似值).
四、综合题
-
16. “一缕清风银叶转”,某市20台风机依次矗立在云遮雾绕的山脊之上,风叶转动,风能就能转换成电能,造福千家万户.某中学初三数学兴趣小组,为测量风叶的长度进行了实地测量.如图,三片风叶两两所成的角为 , 当其中一片风叶与塔干叠合时,在与塔底D水平距离为60米的E处,测得塔顶部O的仰角 , 风叶的视角 .
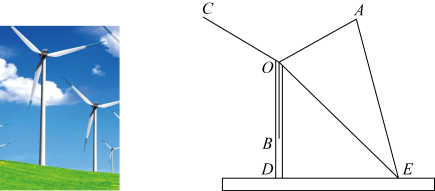 (1)、已知α,β两角和的余弦公式为: , 请利用公式计算;(2)、求风叶的长度.17. 为测量学校后山高度,数学兴趣小组活动过程如下:
(1)、已知α,β两角和的余弦公式为: , 请利用公式计算;(2)、求风叶的长度.17. 为测量学校后山高度,数学兴趣小组活动过程如下: (1)、测量坡角
(1)、测量坡角如图1,后山一侧有三段相对平直的山坡 , 山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)、测量山高同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求 , 小熠同学在作业本上画了一个含角的(如图3),量得 . 求山高 . ( , 结果精确到1米)
(3)、测量改进由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.

如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆 , 使点N,P,D共线,测得的度数,从而得到山顶仰角 , 向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高 . (结果用不含的字母表示)