2023年四川省中考数学真题分类汇编:圆
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 为增强班级凝聚力,吴老师组织开展了一次主题班会.班会上,他设计了一个如图的飞镖靶盘,靶盘由两个同心圆构成,小圆半径为 , 大圆半径为 , 每个扇形的圆心角为60度.如果用飞镖击中靶盘每一处是等可能的,那么小全同学任意投掷飞镖1次(击中边界或没有击中靶盘,则重投1次),投中“免一次作业”的概率是( )
 A、 B、 C、 D、2. 如图,已知点在上,为的中点.若 , 则等于( )
A、 B、 C、 D、2. 如图,已知点在上,为的中点.若 , 则等于( ) A、 B、 C、 D、3. 《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,是以点O为圆心、为半径的圆弧,N是的中点, . “会圆术”给出的弧长的近似值计算公式: . 当 , 时,则的值为( )
A、 B、 C、 D、3. 《梦溪笔谈》是我国古代科技著作,其中它记录了计算圆弧长度的“会圆术”.如图,是以点O为圆心、为半径的圆弧,N是的中点, . “会圆术”给出的弧长的近似值计算公式: . 当 , 时,则的值为( ) A、 B、 C、 D、4. 如图,在中, , 则( )
A、 B、 C、 D、4. 如图,在中, , 则( ) A、1 B、2 C、 D、45. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )
A、1 B、2 C、 D、45. 如图,在中, , 点在斜边上,以为直径的半圆与相切于点 , 与相交于点 , 连接 . 若 , , 则的长是( )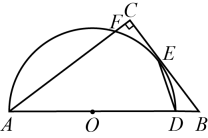 A、 B、 C、 D、6. 如图,内接于 , 是的直径,连接 , , 则的度数是( )
A、 B、 C、 D、6. 如图,内接于 , 是的直径,连接 , , 则的度数是( )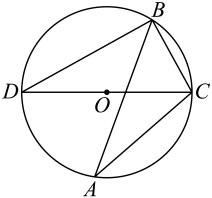 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如图,是的直径,点D,M分别是弦 , 弧的中点, , 则的长是 .
 8. 为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出. 该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳名观众同时观看演出.(取3.14,取1.73)
8. 为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出. 该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳名观众同时观看演出.(取3.14,取1.73) 9. 如图,小珍同学用半径为 , 圆心角为的扇形纸片,制作一个底面半径为的圆锥侧面,则圆锥上粘贴部分的面积是 .
9. 如图,小珍同学用半径为 , 圆心角为的扇形纸片,制作一个底面半径为的圆锥侧面,则圆锥上粘贴部分的面积是 . 10. 如图, , 半径为2的与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设 , 则t的取值范围是 .
10. 如图, , 半径为2的与角的两边相切,点P是⊙O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设 , 则t的取值范围是 .
三、综合题
-
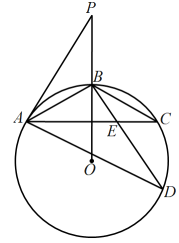
11. 如图,为的直径,C为上一点,连接 , 过点C作的切线交延长线于点D,于点E,交于点F.
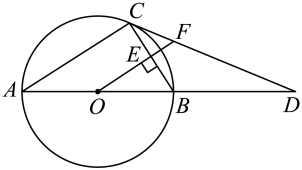 (1)、求证:;(2)、若 , , 求的长.12. 如图,已知是的外接圆, , D是圆上一点,E是DC延长线上一点,连结AD,AE,且 .
(1)、求证:;(2)、若 , , 求的长.12. 如图,已知是的外接圆, , D是圆上一点,E是DC延长线上一点,连结AD,AE,且 . (1)、求证:直线AE是是的切线;(2)、若 , 的半径为3,求AD的长.13. 如图,以为直径的上有两点、 , , 过点作直线交的延长线于点 , 交的延长线于点 , 过作平分交于点 , 交于点 .
(1)、求证:直线AE是是的切线;(2)、若 , 的半径为3,求AD的长.13. 如图,以为直径的上有两点、 , , 过点作直线交的延长线于点 , 交的延长线于点 , 过作平分交于点 , 交于点 . (1)、求证:是的切线;(2)、求证:;(3)、如果是的中点,且 , 求的长.
(1)、求证:是的切线;(2)、求证:;(3)、如果是的中点,且 , 求的长.