2023年四川省中考数学真题分类汇编:三角形(2)
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 如图,在等腰直角中, , 以点为圆心,为半径画弧,交于点 , 以点为圆心,为半径画弧,交于点 , 则图中阴影部分的面积是( )
 A、 B、 C、 D、2. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交于点M,N,再分别以M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线与交于点D, , 垂足为E.则下列结论错误的是( )
A、 B、 C、 D、2. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交于点M,N,再分别以M,N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线与交于点D, , 垂足为E.则下列结论错误的是( )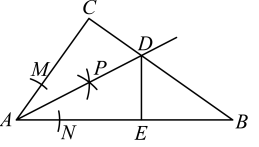 A、 B、 C、 D、3. 如图,在等腰中, , 分别以点点为圆心,大于为半径画弧,两弧分别交于点和点 , 连接 , 直线与交于点 , 连接 , 则的度数是( )
A、 B、 C、 D、3. 如图,在等腰中, , 分别以点点为圆心,大于为半径画弧,两弧分别交于点和点 , 连接 , 直线与交于点 , 连接 , 则的度数是( ) A、 B、 C、 D、4. 如图,在和中,点E、F在上, , , 添加下列条件仍无法证明的是( )
A、 B、 C、 D、4. 如图,在和中,点E、F在上, , , 添加下列条件仍无法证明的是( ) A、 B、 C、 D、5. 《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数 , , 的计算公式: , , , 其中 , , 是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )A、3,4,5 B、5,12,13 C、6,8,10 D、7,24,256. 第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角 , 算出这个正多边形的边数是( )
A、 B、 C、 D、5. 《九章算术》是中国古代重要的数学著作,该著作中给出了勾股数 , , 的计算公式: , , , 其中 , , 是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是( )A、3,4,5 B、5,12,13 C、6,8,10 D、7,24,256. 第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角 , 算出这个正多边形的边数是( )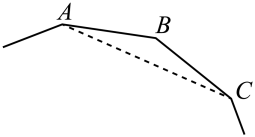 A、9 B、10 C、11 D、12
A、9 B、10 C、11 D、12二、填空题
-
7. 如图,已知 , 点B,E,C,F依次在同一条直线上. 若 , , 则CF的长为.
 8. 如图,内接于 , 圆的半径为7, , 则弦的长度为 .
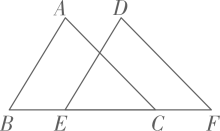
8. 如图,内接于 , 圆的半径为7, , 则弦的长度为 . 9. 如图,中,为对角线,分别以点A、B为圆心,以大于的长为半径画弧,两弧相交于点M、N,作直线交于点E,交于点F,若 , , , 则的长为 .
9. 如图,中,为对角线,分别以点A、B为圆心,以大于的长为半径画弧,两弧相交于点M、N,作直线交于点E,交于点F,若 , , , 则的长为 . 10. 如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若 , 则 .
10. 如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若 , 则 . 11. 如图,在中, , CD平分交AB于点D,过D作交AC于点E,将沿DE折叠得到 , DF交AC于点G.若 , 则.
11. 如图,在中, , CD平分交AB于点D,过D作交AC于点E,将沿DE折叠得到 , DF交AC于点G.若 , 则. 12. 如图,边长为2的等边的两个顶点分别在两条射线上滑动,若 , 则的最大值是 .
12. 如图,边长为2的等边的两个顶点分别在两条射线上滑动,若 , 则的最大值是 . 13. 如图,是正方形边的中点,是正方形内一点,连接 , 线段以为中心逆时针旋转得到线段 , 连接 . 若 , , 则的最小值为 .
13. 如图,是正方形边的中点,是正方形内一点,连接 , 线段以为中心逆时针旋转得到线段 , 连接 . 若 , , 则的最小值为 . 14. 在中, , , 在边上有一点 , 且 , 连接 , 则的最小值为 .15. 如图,在纸片中, , 是边上的中线,将沿折叠,当点落在点处时,恰好 , 若 , 则 .
14. 在中, , , 在边上有一点 , 且 , 连接 , 则的最小值为 .15. 如图,在纸片中, , 是边上的中线,将沿折叠,当点落在点处时,恰好 , 若 , 则 .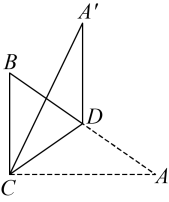
三、综合题
-
16. 如图9,在中, , 点D为AB边上任意一点(不与点A、B重合),过点D作 , , 分别交AC、BC于点E、F,连结EF.
 (1)、求证:四边形ECFD是矩形;(2)、若 , 求点C到EF的距离.17. 如图1,一大一小两个等腰直角三角形叠放在一起, , 分别是斜边 , 的中点, .
(1)、求证:四边形ECFD是矩形;(2)、若 , 求点C到EF的距离.17. 如图1,一大一小两个等腰直角三角形叠放在一起, , 分别是斜边 , 的中点, . (1)、将绕顶点旋转一周,请直接写出点 , 距离的最大值和最小值;(2)、将绕顶点逆时针旋转(如图),求的长.18. 如图1,已知线段 , , 线段绕点在直线上方旋转,连接 , 以为边在上方作 , 且 .
(1)、将绕顶点旋转一周,请直接写出点 , 距离的最大值和最小值;(2)、将绕顶点逆时针旋转(如图),求的长.18. 如图1,已知线段 , , 线段绕点在直线上方旋转,连接 , 以为边在上方作 , 且 . (1)、若 , 以为边在上方作 , 且 , , 连接 , 用等式表示线段与的数量关系是 ;(2)、如图2,在(1)的条件下,若 , , , 求的长;(3)、如图3,若 , , , 当的值最大时,求此时的值.
(1)、若 , 以为边在上方作 , 且 , , 连接 , 用等式表示线段与的数量关系是 ;(2)、如图2,在(1)的条件下,若 , , , 求的长;(3)、如图3,若 , , , 当的值最大时,求此时的值.

