2023年四川省中考数学真题分类汇编:三角形(1)
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 下列说法正确的是( )A、三角形的一个外角等于两个内角的和 B、对角线相等且互相垂直的四边形是正方形 C、在一组数据11,9,7,8,6,8,12,8中,众数和中位数都是8 D、甲乙两组各10名同学参加“安全知识竞赛”,若两组同学的平均成绩相同,甲组的方差 , 乙组的方差 , 则甲组同学的成绩比乙组同学的成绩稳定2. 如图,中, , 则的度数为( )
 A、 B、 C、 D、3. 如图,在中, , 点P为线段上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作于点M、作于点N,连接 , 线段的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为( )
A、 B、 C、 D、3. 如图,在中, , 点P为线段上的动点,以每秒1个单位长度的速度从点A向点B移动,到达点B时停止.过点P作于点M、作于点N,连接 , 线段的长度y与点P的运动时间t(秒)的函数关系如图所示,则函数图象最低点E的坐标为( ) A、 B、 C、 D、4. 如图2,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若 , 则( )
A、 B、 C、 D、4. 如图2,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若 , 则( ) A、2 B、 C、3 D、45. 我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( )
A、2 B、 C、3 D、45. 我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( ) A、 B、 C、 D、6. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )
A、 B、 C、 D、6. 如图,在正方形中,点E是上一点,延长至点F,使 , 连结 , 交于点K,过点A作 , 垂足为点H,交于点G,连结 . 下列四个结论:①;②;③;④ . 其中正确结论的个数为( )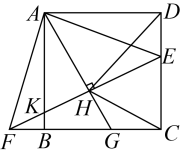 A、1个 B、2个 C、3个 D、4个7. 如图,边长为6的正方形中,M为对角线上的一点,连接并延长交于点P.若 , 则的长为( )
A、1个 B、2个 C、3个 D、4个7. 如图,边长为6的正方形中,M为对角线上的一点,连接并延长交于点P.若 , 则的长为( ) A、 B、 C、 D、8. 如图,和是以点为直角顶点的等腰直角三角形,把以为中心顺时针旋转,点为射线、的交点.若 , . 以下结论:
A、 B、 C、 D、8. 如图,和是以点为直角顶点的等腰直角三角形,把以为中心顺时针旋转,点为射线、的交点.若 , . 以下结论:①;②;
③当点在的延长线上时,;
④在旋转过程中,当线段最短时,的面积为 .
其中正确结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,在平面直角坐标系中,已知点 , 点 , 点在轴上,且点在点右方,连接 , , 若 , 则点的坐标为 .
 10. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形中, , , 对角线与交于点O,点E为边上的一个动点, , , 垂足分别为点F,G,则 .
10. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形中, , , 对角线与交于点O,点E为边上的一个动点, , , 垂足分别为点F,G,则 . 11. 如图,中,是中线,分别以点A,点B为圆心,大于长为半径作弧,两孤交于点M,N.直线交于点E.连接交于点F.过点D作 , 交于点G.若 , 则的长为 .
11. 如图,中,是中线,分别以点A,点B为圆心,大于长为半径作弧,两孤交于点M,N.直线交于点E.连接交于点F.过点D作 , 交于点G.若 , 则的长为 . 12. 若三角形三个内角的比为1:2:3,则这个三角形按角分类是三角形.13. 如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 .
12. 若三角形三个内角的比为1:2:3,则这个三角形按角分类是三角形.13. 如图,四边形是边长为4的正方形,是等边三角形,则阴影部分的面积为 . 14. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号)
14. 如图,在等边中,过点C作射线 , 点M,N分别在边 , 上,将沿折叠,使点B落在射线上的点处,连接 , 已知 . 给出下列四个结论:①为定值;②当时,四边形为菱形;③当点N与C重合时,;④当最短时, . 其中正确的结论是(填写序号) 15. 如图,以的边、为腰分别向外作等腰直角、 , 连结、、 , 过点的直线分别交线段、于点、 , 以下说法:①当时,;②;③若 , , , 则;④当直线时,点为线段的中点.正确的有 . (填序号)
15. 如图,以的边、为腰分别向外作等腰直角、 , 连结、、 , 过点的直线分别交线段、于点、 , 以下说法:①当时,;②;③若 , , , 则;④当直线时,点为线段的中点.正确的有 . (填序号)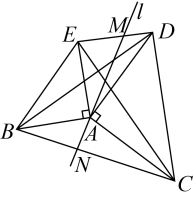
三、综合题
-
16. 如图,在中, .
 (1)、尺规作图:作的角平分线交于点(不写做法,保留作图痕迹);(2)、在(1)所作图形中,求的面积.17. 如图,网格中每个小正方形的边长均为1,的顶点均在小正方形的格点上.
(1)、尺规作图:作的角平分线交于点(不写做法,保留作图痕迹);(2)、在(1)所作图形中,求的面积.17. 如图,网格中每个小正方形的边长均为1,的顶点均在小正方形的格点上. (1)、将向下平移3个单位长度得到 , 画出;(2)、将绕点顺时针旋转90度得到 , 画出;(3)、在(2)的运动过程中请计算出扫过的面积.18. 在学习完《图形的旋转》后,刘老师带领学生开展了一次数学探究活动
(1)、将向下平移3个单位长度得到 , 画出;(2)、将绕点顺时针旋转90度得到 , 画出;(3)、在(2)的运动过程中请计算出扫过的面积.18. 在学习完《图形的旋转》后,刘老师带领学生开展了一次数学探究活动【问题情境】
刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容:
如图,将一个三角形纸板绕点A逆时针旋转到达的位置,那么可以得到:
;( )

刘老师进一步谈到:图形的旋转蕴含于自然界的运动变化规律中,即“变”中蕴含着“不变”,这是我们解决图形旋转的关键故数学就是一门哲学.
(1)、【问题解决】
上述问题情境中“( )”处应填理由:;(2)、如图,小王将一个半径为 , 圆心角为的扇形纸板ABC绕点O逆时针旋转到达扇形纸板的位置.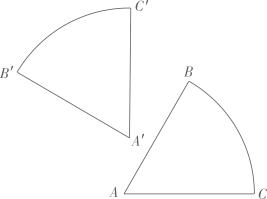
①请在图中作出点O;
②如果 , 则在旋转过程中,点B经过的路径长为;
(3)、【问题拓展】小李突发奇想,将与(2)中完全相同的两个扇形纸板重叠,一个固定在墙上,使得一边位于水平位置另一个在孤的中点处固定,然后放开纸板,使其摆动到竖直位置时静止此时,两个纸板重叠部分的面积是多少呢?如图所示,请你帮助小李解决这个问题.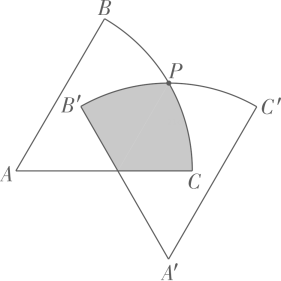 19. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
19. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.在中, , , D是AB边上一点,且(n为正整数),E是AC边上的动点,过点D作DE的垂线交直线BC于点F.
 (1)、【初步感知】
(1)、【初步感知】如图1,当时,兴趣小组探究得出结论: , 请写出证明过程.
(2)、【深入探究】①如图2,当 , 且点F在线段BC上时,试探究线段AE,BF,AB之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段AE,BF,AB之间数量关系的一般结论(直接写出结论,不必证明).
(3)、【拓展运用】如图3,连接EF,设EF的中点为M. 若 , 求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).