2023年四川省中考数学真题分类汇编:图形认识初步、相交线与平行线
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 如图,是的直径,点C,D在上,连接 , 若 , 则的度数是( )
 A、 B、 C、 D、2. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、2. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、3. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( )
A、 B、 C、 D、3. 如图,在中,点D、E为边的三等分点,点F、G在边上, , 点H为与的交点.若 , 则的长为( ) A、1 B、 C、2 D、34. 如图,切于点B,连接交于点C,交于点D,连接 , 若 , 则的度数为( )
A、1 B、 C、2 D、34. 如图,切于点B,连接交于点C,交于点D,连接 , 若 , 则的度数为( ) A、 B、 C、 D、5. 如图, , 且 , , 则等于( )
A、 B、 C、 D、5. 如图, , 且 , , 则等于( ) A、 B、 C、 D、6. 如图, , 平分 , 则( )
A、 B、 C、 D、6. 如图, , 平分 , 则( ) A、 B、 C、 D、7. 下列图形中,是长方体表面展开图的是( )A、
A、 B、 C、 D、7. 下列图形中,是长方体表面展开图的是( )A、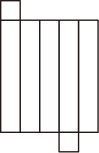 B、
B、 C、
C、 D、
D、 8. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, , 则( )
8. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, , 则( ) A、 B、 C、 D、9. 如图,某人沿路线行走,与方向相同, , 则( )
A、 B、 C、 D、9. 如图,某人沿路线行走,与方向相同, , 则( )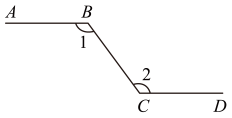 A、 B、 C、 D、10. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )
A、 B、 C、 D、10. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )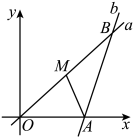 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
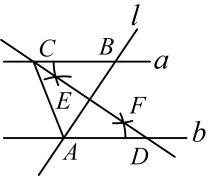
11. 如图, , 直线l与直线a,b分别交于B,A两点,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点E,F,作直线 , 分别交直线a,b于点C,D,连接AC,若 , 则的度数为 .
 12. 如图,圆柱形玻璃杯的杯高为 , 底面周长为 , 在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 , 且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为 . (杯壁厚度不计)
12. 如图,圆柱形玻璃杯的杯高为 , 底面周长为 , 在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 , 且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为 . (杯壁厚度不计)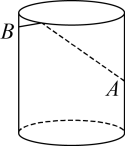 13. 如图,点O在直线AB上,OD是的平分线,若 , 则的度数为 .
13. 如图,点O在直线AB上,OD是的平分线,若 , 则的度数为 . 14. 如图,在中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;②以点D为圆心,以AM长为半径作弧,交DB于点;③以点为圆心,以MN长为半径作弧,在内部交前面的弧于点;④过点作射线交BC于点E. 若与四边形ACED的面积比为4:21,则的值为.
14. 如图,在中,D是边AB上一点,按以下步骤作图:①以点A为圆心,以适当长为半径作弧,分别交AB,AC于点M,N;②以点D为圆心,以AM长为半径作弧,交DB于点;③以点为圆心,以MN长为半径作弧,在内部交前面的弧于点;④过点作射线交BC于点E. 若与四边形ACED的面积比为4:21,则的值为.
三、解答题
-
15. 如图,点在线段上, , , . 求证: .
 16. 如图,在四边形中,与交于点 , , 垂足分别为点 , 且 . 求证:四边形是平行四边形.
16. 如图,在四边形中,与交于点 , , 垂足分别为点 , 且 . 求证:四边形是平行四边形. 17. 如图,已知AB与CD相交于点O, , 求证: .
17. 如图,已知AB与CD相交于点O, , 求证: . 18. 已知:如图, , , . 求证: .
18. 已知:如图, , , . 求证: .
四、综合题
-
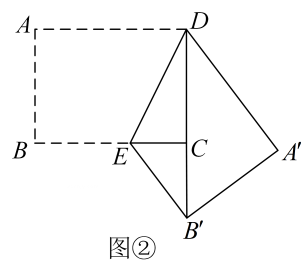
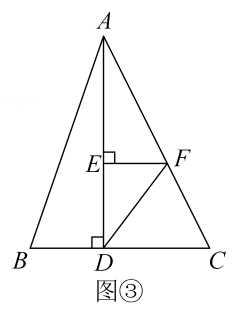
19. 如图,在中,D是的中点,E是的中点,过点A作交的延长线于点F.
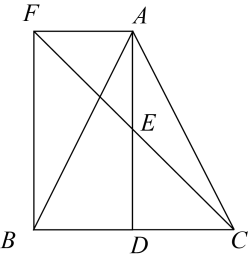 (1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.20. 如图,以的直角边为直径作 , 交斜边于点 , 点是的中点,连接 .
(1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.20. 如图,以的直角边为直径作 , 交斜边于点 , 点是的中点,连接 . (1)、求证:是的切线.(2)、若 , 求的长.(3)、求证: .21. 如图,在中,点 , 在对角线上, . 求证:
(1)、求证:是的切线.(2)、若 , 求的长.(3)、求证: .21. 如图,在中,点 , 在对角线上, . 求证: (1)、;(2)、 .22. 如图,中,点E是的中点,连接并延长交的延长线于点F.
(1)、;(2)、 .22. 如图,中,点E是的中点,连接并延长交的延长线于点F. (1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.23. 如图,四边形中, , 点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)、求证:;(2)、点G是线段上一点,满足 , 交于点H,若 , 求的长.23. 如图,四边形中, , 点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合) (1)、求证:;(2)、当直线时,连接、 , 试判断四边形的形状,并说明理由.24. 如图,以的边AC为直径作 , 交BC边于点D,过点C作交于点E,连接AD,DE,.
(1)、求证:;(2)、当直线时,连接、 , 试判断四边形的形状,并说明理由.24. 如图,以的边AC为直径作 , 交BC边于点D,过点C作交于点E,连接AD,DE,. (1)、求证:;(2)、若 , , 求AB和DE的长.25. 如图,以线段为直径作 , 交射线于点C,平分交于点D,过点D作直线 , 交的延长线于点E,交的延长线于点F.连接并延长交的延长线于点M.
(1)、求证:;(2)、若 , , 求AB和DE的长.25. 如图,以线段为直径作 , 交射线于点C,平分交于点D,过点D作直线 , 交的延长线于点E,交的延长线于点F.连接并延长交的延长线于点M. (1)、求证:直线是的切线;(2)、当时,判断的形状,并说明理由;(3)、在(2)的条件下, , 连接交于点P,求的长.26. 如图,与相切于点A,半径 , 与相交于点D,连接 .
(1)、求证:直线是的切线;(2)、当时,判断的形状,并说明理由;(3)、在(2)的条件下, , 连接交于点P,求的长.26. 如图,与相切于点A,半径 , 与相交于点D,连接 .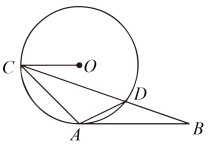 (1)、求证:;(2)、若 , 求的长.27. 如图,中,以为直径的交于点E.平分 , 过点E作于点D,延长交的延长线于点P.
(1)、求证:;(2)、若 , 求的长.27. 如图,中,以为直径的交于点E.平分 , 过点E作于点D,延长交的延长线于点P.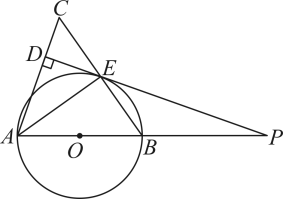 (1)、求证:是的切线;(2)、若 , 求的长.28. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点.
(1)、求证:是的切线;(2)、若 , 求的长.28. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点. (1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.
(1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.