2023年四川省中考数学真题分类汇编:反比例函数
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 如图,在平面直角坐标系中,点A、B分别在y,x轴上,轴.点M、N分别在线段、上, , , 反比例函数的图象经过M、N两点,P为x正半轴上一点,且 , 的面积为3,则k的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
2. 若点 , 都在反比例函数的图象上,则(填“>”或“<”).3. 如图,一次函数与反比例函数的图象相交于两点,以为边作等边三角形 , 若反比例函数的图象过点 , 则的值为 .
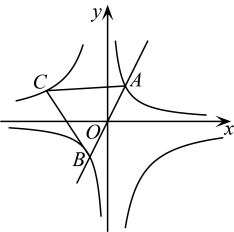 4. 如图,在平面直角坐标系中,O为坐标原点,垂直于x轴,以为对称轴作的轴对称图形,对称轴与线段相交于点F,点D的对应点B恰好落在反比例函数的图象上,点O、E的对应点分别是点C、A.若点A为的中点,且 , 则k的值为 .
4. 如图,在平面直角坐标系中,O为坐标原点,垂直于x轴,以为对称轴作的轴对称图形,对称轴与线段相交于点F,点D的对应点B恰好落在反比例函数的图象上,点O、E的对应点分别是点C、A.若点A为的中点,且 , 则k的值为 .
三、综合题
-
5. 如图,在平面直角坐标系中,直线与x轴交于点 , 与y轴交于点 , 与反比例函数在第四象限内的图象交于点 .
 (1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.6. 如图,点在反比例函数图象上.一次函数的图象经过点A,分别交x轴,y轴于点B,C,且与的面积比为 .
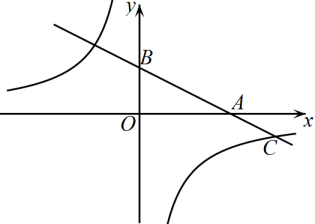
(1)、求反比例函数的表达式:(2)、当时,直接写出x的取值范围;(3)、在双曲线上是否存在点P,使是以点A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.6. 如图,点在反比例函数图象上.一次函数的图象经过点A,分别交x轴,y轴于点B,C,且与的面积比为 . (1)、求反比例函数和一次函数的解析式;(2)、请直接写出时,x的取值范围.7. 如图,一次函数的图象与反比例函数的图象交于点 , 与x轴交于点B, 与y轴交于点 .
(1)、求反比例函数和一次函数的解析式;(2)、请直接写出时,x的取值范围.7. 如图,一次函数的图象与反比例函数的图象交于点 , 与x轴交于点B, 与y轴交于点 . (1)、求m的值和一次函数的表达式;(2)、已知P为反比例函数图象上的一点, , 求点P的坐标.8. 如图,一次函数的图像与反比例函数的图像交于 , 两点.( , , 为常数)
(1)、求m的值和一次函数的表达式;(2)、已知P为反比例函数图象上的一点, , 求点P的坐标.8. 如图,一次函数的图像与反比例函数的图像交于 , 两点.( , , 为常数) (1)、求一次函数和反比例函数的解析式;(2)、根据图像直接写出不等式的解集;(3)、为轴上一点,若的面积为 , 求点的坐标.9. 如图,在平面直角坐标系中,等腰直角三角形的直角顶点 , 顶点A、恰好落在反比例函数第一象限的图象上.
(1)、求一次函数和反比例函数的解析式;(2)、根据图像直接写出不等式的解集;(3)、为轴上一点,若的面积为 , 求点的坐标.9. 如图,在平面直角坐标系中,等腰直角三角形的直角顶点 , 顶点A、恰好落在反比例函数第一象限的图象上. (1)、分别求反比例函数的表达式和直线所对应的一次函数的表达式;(2)、在x轴上是否存在一点P,使周长的值最小.若存在,求出最小值;若不存在,请说明理由.10. 如图,在平面直角坐标系xOy中,直线与y轴交于点A,与反比例函数的图象的一个交点为 , 过点B作AB的垂线l.
(1)、分别求反比例函数的表达式和直线所对应的一次函数的表达式;(2)、在x轴上是否存在一点P,使周长的值最小.若存在,求出最小值;若不存在,请说明理由.10. 如图,在平面直角坐标系xOy中,直线与y轴交于点A,与反比例函数的图象的一个交点为 , 过点B作AB的垂线l. (1)、求点A的坐标及反比例函数的表达式;(2)、若点C在直线l上,且的面积为5,求点C的坐标;(3)、P是直线l上一点,连接PA,以P为位似中心画 , 使它与位似,相似比为m.若点D,E恰好都落在反比例函数图象上,求点P的坐标及m的值.11. 阅读理解题:
(1)、求点A的坐标及反比例函数的表达式;(2)、若点C在直线l上,且的面积为5,求点C的坐标;(3)、P是直线l上一点,连接PA,以P为位似中心画 , 使它与位似,相似比为m.若点D,E恰好都落在反比例函数图象上,求点P的坐标及m的值.11. 阅读理解题:阅读材料:
如图1,四边形是矩形,是等腰直角三角形,记为、为 , 若 , 则 .

证明:设 , ∵ , ∴ ,
易证
∴ ,
∴
∴ ,
若时,当 , 则 .
同理:若时,当 , 则 .
根据上述材料,完成下列问题:
如图2,直线与反比例函数的图象交于点 , 与轴交于点 . 将直线绕点顺时针旋转后的直线与轴交于点 , 过点作轴于点 , 过点作轴于点 , 已知 .
 (1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.12. 如图,在平面直角坐标系中,直线与 , 轴分别相交于点A,B,与反比例函数的图象相交于点C,已知 , 点C的横坐标为2.
(1)、求反比例函数的解析式;(2)、直接写出的值;(3)、求直线的解析式.12. 如图,在平面直角坐标系中,直线与 , 轴分别相交于点A,B,与反比例函数的图象相交于点C,已知 , 点C的横坐标为2. (1)、求 , 的值;(2)、平行于轴的动直线与和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.
(1)、求 , 的值;(2)、平行于轴的动直线与和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.
-