2023年四川省中考数学真题分类汇编:一次函数
试卷更新日期:2023-07-30 类型:二轮复习
一、选择题
-
1. 如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( )
2. 在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( ) A、 B、 C、 D、3. 下列各点在函数图象上的是( )A、 B、 C、 D、4. 如图1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是( )
A、 B、 C、 D、3. 下列各点在函数图象上的是( )A、 B、 C、 D、4. 如图1,小亮家、报亭、羽毛球馆在一条直线上.小亮从家跑步到羽毛球馆打羽毛球,再去报亭看报,最后散步回家.小亮离家距离y与时间x之间的关系如图2所示.下列结论错误的是( ) A、小亮从家到羽毛球馆用了分钟 B、小亮从羽毛球馆到报亭平均每分钟走米 C、报亭到小亮家的距离是米 D、小亮打羽毛球的时间是分钟5. 如图5,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,C、D是半径为1的上两动点,且 , P为弦CD的中点.当C、D两点在圆上运动时,面积的最大值是( )
A、小亮从家到羽毛球馆用了分钟 B、小亮从羽毛球馆到报亭平均每分钟走米 C、报亭到小亮家的距离是米 D、小亮打羽毛球的时间是分钟5. 如图5,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,C、D是半径为1的上两动点,且 , P为弦CD的中点.当C、D两点在圆上运动时,面积的最大值是( )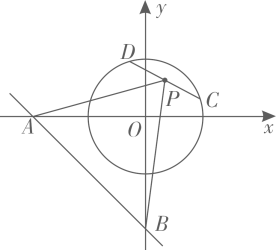 A、8 B、6 C、4 D、3
A、8 B、6 C、4 D、3二、填空题
-
6. 如图,直线(k为常数,)与x,y轴分别交于点A,B,则的值是 .
 7. 如图,在平面直角坐标系中,点B的坐标为 , 过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线与交于点D.与y轴交于点E.动点M在线段上,动点N在直线上,若是以点N为直角顶点的等腰直角三角形,则点M的坐标为
7. 如图,在平面直角坐标系中,点B的坐标为 , 过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线与交于点D.与y轴交于点E.动点M在线段上,动点N在直线上,若是以点N为直角顶点的等腰直角三角形,则点M的坐标为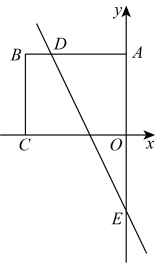 8. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .
8. 如图,直线与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线上的一动点,动点 , 连接 . 当取最小值时,的最小值是 .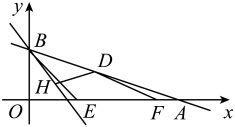
三、综合题
-
9. 如图,已知一次函数的图象与反比例函数的图象交于 , B两点,与x轴交于点C,将直线沿y轴向上平移3个单位长度后与反比例函数图象交于点D,E.
 (1)、求k,m的值及C点坐标;(2)、连接 , , 求的面积.10. 如图,在平面直角坐标系中,一次函数与反比例函数的图象在第一象限内交于和两点,直线与x轴相交于点C,连接 .
(1)、求k,m的值及C点坐标;(2)、连接 , , 求的面积.10. 如图,在平面直角坐标系中,一次函数与反比例函数的图象在第一象限内交于和两点,直线与x轴相交于点C,连接 . (1)、求一次函数与反比例函数的表达式;(2)、当时,请结合函数图象,直接写出关于x的不等式的解集;(3)、过点B作平行于x轴,交于点D,求梯形的面积.11. 如图,一次函数(为常数,)的图象与反比例函数为常数,的图象在第一象限交于点 , 与轴交于点 .
(1)、求一次函数与反比例函数的表达式;(2)、当时,请结合函数图象,直接写出关于x的不等式的解集;(3)、过点B作平行于x轴,交于点D,求梯形的面积.11. 如图,一次函数(为常数,)的图象与反比例函数为常数,的图象在第一象限交于点 , 与轴交于点 .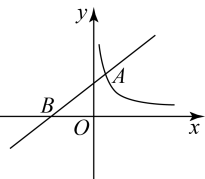 (1)、求一次函数和反比例函数的解析式.(2)、点在轴上,是以为腰的等腰三角形,请直接写出点的坐标.12. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D.
(1)、求一次函数和反比例函数的解析式.(2)、点在轴上,是以为腰的等腰三角形,请直接写出点的坐标.12. 如图,一次函数图象与反比例函数图象交于点 , , 与x轴交于点C,与y轴交于点D. (1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.13. 某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且 , 售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式(1)、若产销A,B两种产品的日利润分别为元,元,请分别写出 , 与x的函数关系式,并写出x的取值范围;(2)、分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)(3)、为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】14. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售,经了解.每个乙种粽子的进价比每个甲种粽子的进价多2元,用1000元购进甲种粽子的个数与用1200元购进乙种粽子的个数相同.(1)、甲、乙两种粽子每个的进价分别是多少元?(2)、该超市计划购进这两种粽子共200个(两种都有),其中甲种粽子的个数不低于乙种粽子个数的2倍,若甲、乙两种粽子的售价分别为12元/个、15元/个,设购进甲种粽子m个,两种粽子全部售完时获得的利润为w元.
(1)、求反比例函数与一次函数的解析式;(2)、点M在x轴上,若 , 求点M的坐标.13. 某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且 , 售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式(1)、若产销A,B两种产品的日利润分别为元,元,请分别写出 , 与x的函数关系式,并写出x的取值范围;(2)、分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)(3)、为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】14. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售,经了解.每个乙种粽子的进价比每个甲种粽子的进价多2元,用1000元购进甲种粽子的个数与用1200元购进乙种粽子的个数相同.(1)、甲、乙两种粽子每个的进价分别是多少元?(2)、该超市计划购进这两种粽子共200个(两种都有),其中甲种粽子的个数不低于乙种粽子个数的2倍,若甲、乙两种粽子的售价分别为12元/个、15元/个,设购进甲种粽子m个,两种粽子全部售完时获得的利润为w元.①求w与m的函数关系式,并求出m的取值范围;
②超市应如何进货才能获得最大利润,最大利润是多少元?
15. 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行. “当好东道主,热情迎嘉宾”,成都某知名小吃店计划购买A,B两种食材制作小吃. 已知购买1千克A种食材和1千克B种食材共需68元,购买5千克A种食材和3千克B种食材共需280元.(1)、求A,B两种食材的单价;(2)、该小吃店计划购买两种食材共36千克,其中购买A种食材千克数不少于B种食材千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.16. 某移动公司推出A,B两种电话计费方式.计费方式
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
A
免费
B
免费
(1)、设一个月内用移动电话主叫时间为tmin,根据上表,分别写出在不同时间范围内,方式A,方式B的计费金额关于t的函数解析式;(2)、若你预计每月主叫时间为350min,你将选择A,B哪种计费方式,并说明理由;(3)、请你根据月主叫时间t的不同范围,直接写出最省钱的计费方式.17. 如图,在平面直角坐标系中,抛物线与x轴交于 , 两点.与y轴交于点 .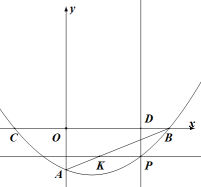 (1)、求该抛物线的函数表达式;(2)、若点P是直线下方抛物线上的一动点,过点P作x轴的平行线交于点K,过点P作y轴的平行线交x轴于点D,求与的最大值及此时点P的坐标;(3)、在抛物线的对称轴上是否存在一点M,使得是以为一条直角边的直角三角形:若存在,请求出点M的坐标,若不存在,请说明理由.18. 如图,二次函数的图象交轴于点 , 交轴于点 , 点的坐标为 , 对称轴是直线 , 点是轴上一动点,轴,交直线于点 , 交抛物线于点 .
(1)、求该抛物线的函数表达式;(2)、若点P是直线下方抛物线上的一动点,过点P作x轴的平行线交于点K,过点P作y轴的平行线交x轴于点D,求与的最大值及此时点P的坐标;(3)、在抛物线的对称轴上是否存在一点M,使得是以为一条直角边的直角三角形:若存在,请求出点M的坐标,若不存在,请说明理由.18. 如图,二次函数的图象交轴于点 , 交轴于点 , 点的坐标为 , 对称轴是直线 , 点是轴上一动点,轴,交直线于点 , 交抛物线于点 . (1)、求这个二次函数的解析式.(2)、若点在线段上运动(点与点、点不重合),求四边形面积的最大值,并求出此时点的坐标.(3)、若点在轴上运动,则在轴上是否存在点 , 使以、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.19. 如图1,抛物线()与轴交于 , 两点,与轴交于点 .
(1)、求这个二次函数的解析式.(2)、若点在线段上运动(点与点、点不重合),求四边形面积的最大值,并求出此时点的坐标.(3)、若点在轴上运动,则在轴上是否存在点 , 使以、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.19. 如图1,抛物线()与轴交于 , 两点,与轴交于点 . (1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.20. 端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,每千克A粽子节前的进价比节后多2元,节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克.根据以上信息,解答下列问题:(1)、该商场节后每千克A粽子的进价是多少元?(2)、如果该商场在节前和节后共购进A粽子400千克,且总费用不超过4600元,并按照节前每千克20元,节后每千克16元全部售出,那么该商场节前购进多少千克A粽子获得利润最大?最大利润是多少?
(1)、求抛物线的解析式;(2)、点P在抛物线上,点Q在x轴上,以B,C,P,Q为顶点的四边形为平行四边形,求点P的坐标;(3)、如图2,抛物线顶点为D,对称轴与x轴交于点E,过点的直线(直线除外)与抛物线交于G,H两点,直线 , 分别交x轴于点M,N.试探究是否为定值,若是,求出该定值;若不是,说明理由.20. 端午节是中国传统节日,人们有吃粽子的习俗.今年端午节来临之际,某商场预测A粽子能够畅销.根据预测,每千克A粽子节前的进价比节后多2元,节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克.根据以上信息,解答下列问题:(1)、该商场节后每千克A粽子的进价是多少元?(2)、如果该商场在节前和节后共购进A粽子400千克,且总费用不超过4600元,并按照节前每千克20元,节后每千克16元全部售出,那么该商场节前购进多少千克A粽子获得利润最大?最大利润是多少?