北师大版数学九年级上册同步练习——第五章《投影与视图》综合训练A
试卷更新日期:2023-07-29 类型:单元试卷
一、选择题(每题3分,共36分)
-
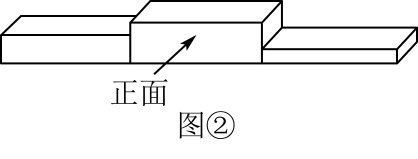
1. 图①是2023年6月11日吉林市全程马拉松男子组颁奖现场.图②是领奖台的示意图,则此领奖台的主视图是( )

 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )
2. 如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是( )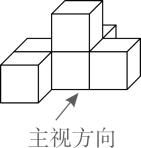 A、2 B、3 C、4 D、53. 如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )
A、2 B、3 C、4 D、53. 如图是一个由6个相同的正方体组成的立体图形,它的主视图是( )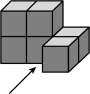 A、
A、 B、
B、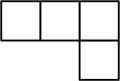 C、
C、 D、
D、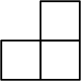 4. 下列几何体中,三视图都是圆的是( )A、长方体 B、图柱 C、圆锥 D、球5. 几个大小相同的小正方体搭成几何体的俯视图如图所示,图中小正方形中数字表示对应位置小正方体的个数,该几何体的主视图是( )
4. 下列几何体中,三视图都是圆的是( )A、长方体 B、图柱 C、圆锥 D、球5. 几个大小相同的小正方体搭成几何体的俯视图如图所示,图中小正方形中数字表示对应位置小正方体的个数,该几何体的主视图是( ) A、
A、 B、
B、 C、
C、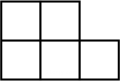 D、
D、 6. 榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
6. 榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )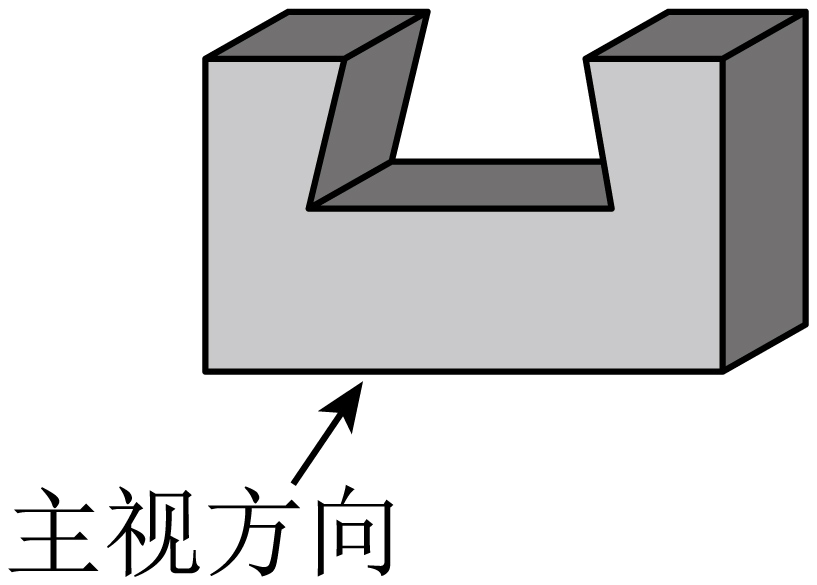 A、
A、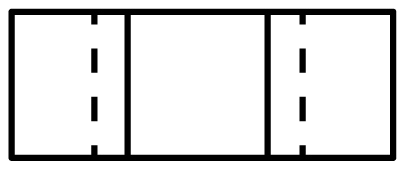 B、
B、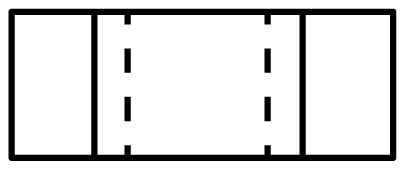 C、
C、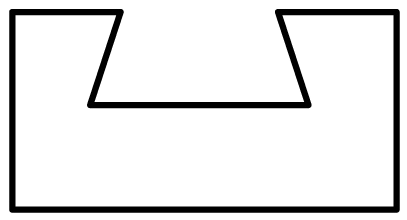 D、
D、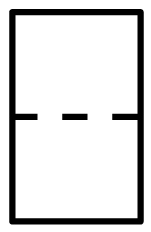 7. 作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从左面看到的图形的是( )
7. 作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从左面看到的图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,对正方体进行两次切割,得到如图⑤所示的几何体,则图⑤几何体的俯视图为( )
8. 如图,对正方体进行两次切割,得到如图⑤所示的几何体,则图⑤几何体的俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )
9. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )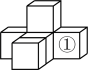 A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变10. 一个矩形木框在地面上形成的投影不可能是( )A、
A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变10. 一个矩形木框在地面上形成的投影不可能是( )A、 B、
B、 C、
C、 D、
D、 11. 下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )A、
11. 下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )A、 B、
B、 C、
C、 D、
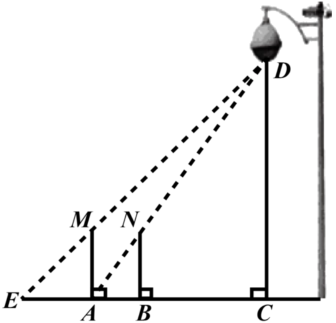
D、 12. 如图,身高为1.6 m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2 m,AB=10 m,则旗杆的高度是( )
12. 如图,身高为1.6 m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2 m,AB=10 m,则旗杆的高度是( ) A、6.4m B、7m C、8m D、9m
A、6.4m B、7m C、8m D、9m二、填空题(每题3分,共18分)
-
13. 公元前6世纪,古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2,小明仿照这个方法,测量圆锥形小山包的高度,已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒,当木棒影子长度等于木棒高度时,测得小山包影子AB长为23 m(直线AB过底面圆心),则小山包的高为m(π取3.14).

 14. 数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为米.
14. 数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为1.2米,落在地面上的影长为2.4米,则树高为米. 15. 若一个几何体由若干大小相同的小立方体搭成,如图分别是从它的左视图与俯视图,该几何体所用小立方体的个数是 , 则的最小值是.
15. 若一个几何体由若干大小相同的小立方体搭成,如图分别是从它的左视图与俯视图,该几何体所用小立方体的个数是 , 则的最小值是.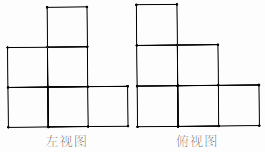 16. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为 .
16. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为 .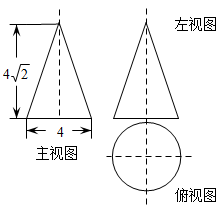 17. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm.
17. 三棱柱的三视图如图所示,在俯视图△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则左视图中AB的长为cm. 18. 一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块个.
18. 一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,那么搭成该几何体至少需用小立方块个.
三、解答题(共7题,共66分)
-
19. 如图,从上往下看 , , , , , 六个物体,分别能得到 , , , , , 哪个图形?把上下两种对应的图形于物体连接起来.
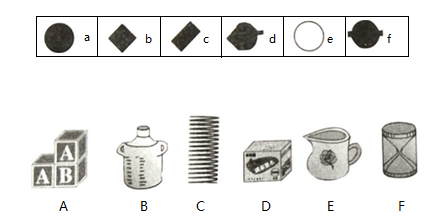 20. 如图,这是一个由大小相等的正方体堆成的几何体的俯视图,小正方形中的数字表示该位置的小正方体的个数,请你画出它的主视图和左视图.
20. 如图,这是一个由大小相等的正方体堆成的几何体的俯视图,小正方形中的数字表示该位置的小正方体的个数,请你画出它的主视图和左视图. 21. 用若干个小立方块搭成一个几何体,使它从正面看与从左面看都是如图的同一个图.通过实际操作,并与同学们讨论,解决下列问题:
21. 用若干个小立方块搭成一个几何体,使它从正面看与从左面看都是如图的同一个图.通过实际操作,并与同学们讨论,解决下列问题:
(1)、所需要的小立方块的个数是多少?你能找出几种?(2)、画出所需个数最少和所需个数最多的几何体从上面看到的图,并在小正方形里注明在该位置上小立方块的个数.
22. 在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼 , 大树的影子有一部分落在地面上,还有一部分落在教学楼的墙上,墙上的影子长为 , 已知此时高的竹竿在水平地面上的影子长 , 那么这棵大树高度是多少?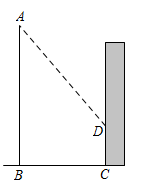 23. 某小组的项目式学习活动内容是测量某棵古树的高度 , 如图,在阳光下,某一时刻,古树的影子落在了地上和围墙上,落在地上的长度米,落在墙上的长度米,在古树的附近有一棵小树 , 同一时刻,小树的影长米,小树的高米.已知点N,P,B,D在一条水平线上, , , , 请求出该古树的高度 .
23. 某小组的项目式学习活动内容是测量某棵古树的高度 , 如图,在阳光下,某一时刻,古树的影子落在了地上和围墙上,落在地上的长度米,落在墙上的长度米,在古树的附近有一棵小树 , 同一时刻,小树的影长米,小树的高米.已知点N,P,B,D在一条水平线上, , , , 请求出该古树的高度 .