2023-2024学年初中数学九年级上册 26.3 二次函数y = ax²+bx+c的图像 同步分层训练培优卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 设二次函数y=x2-kx+2k(k为实数)的图象过点(1,y1),(2,y2),(3,y3),(4,y4),设y1-y2=a,y3-y4=b,( )A、若ab<0,且a+b<0,则k<7 B、若ab<0,且a+b>0,则k<5 C、若ab>0,且a+b<0,则k>3 D、若ab>0,且a+b>0,则k>72. 在平面直角坐标系中,有两条抛物线关于x轴对称,且他们的顶点相距6个单位长度,若其中一条抛物线的解析式为 , 则m的值是( )
 A、 B、 C、或 D、或3. 函数与在同一直角坐标系中的图象大致是( )A、
A、 B、 C、或 D、或3. 函数与在同一直角坐标系中的图象大致是( )A、 B、
B、 C、
C、 D、
D、 4. 下列抛物线中,与抛物线具有相同对称轴的是( )A、 B、 C、 D、5. 已知,二次函数的对称轴为y轴,将此函数向下平移3个单位,若点M为二次函数图象在()部分上任意一点,O为坐标原点,连接 , 则长度的最小值是( )A、 B、2 C、 D、6. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
4. 下列抛物线中,与抛物线具有相同对称轴的是( )A、 B、 C、 D、5. 已知,二次函数的对称轴为y轴,将此函数向下平移3个单位,若点M为二次函数图象在()部分上任意一点,O为坐标原点,连接 , 则长度的最小值是( )A、 B、2 C、 D、6. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( ) A、1.4 B、2.5 C、2.8 D、37. 如图,平面直角坐标系中,已知 , , , 抛物线过点、 , 顶点为 , 抛物线过点 , , 顶点为 , 若点在线段上,则:的值为( )
A、1.4 B、2.5 C、2.8 D、37. 如图,平面直角坐标系中,已知 , , , 抛物线过点、 , 顶点为 , 抛物线过点 , , 顶点为 , 若点在线段上,则:的值为( ) A、 B、 C、 D、8. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
A、 B、 C、 D、8. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
9. 如图,在平面直角坐标系中,抛物线经过平移得到抛物线 , 其对称轴与两段抛物线所围成的阴影部分的面积为 .
 10. 写出一个函数使其图像与反比例函数的图象有3个不同的交点 .11. 二次函数的图象经过点 , 则代数式的值为.12. 已知函数 的图象与函数 的图象恰好有四个交点,则 的取值范围是.13. 如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.
10. 写出一个函数使其图像与反比例函数的图象有3个不同的交点 .11. 二次函数的图象经过点 , 则代数式的值为.12. 已知函数 的图象与函数 的图象恰好有四个交点,则 的取值范围是.13. 如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点. (1)、抛物线的解析式为;(2)、若点D、N均在此抛物线上,其中点D坐标为(2,﹣2),点N满足∠NBO=∠ABO , P为平面上一点,则所有满足△POD∽△NOB的点P的坐标有(点P、O、D分别与点N、O、B对应).
(1)、抛物线的解析式为;(2)、若点D、N均在此抛物线上,其中点D坐标为(2,﹣2),点N满足∠NBO=∠ABO , P为平面上一点,则所有满足△POD∽△NOB的点P的坐标有(点P、O、D分别与点N、O、B对应).三、解答题
-
14. 在等式中,当时,;当时,;时,.求、、的值.15. 求下列二次函数图象的对称轴和顶点坐标: .
四、综合题
-
16. 如图,在平而直角坐标系中,二次函数的图象与轴分别交于点 , 顶点为 . 连接 , 将线段绕点按顺时针方向旋转得到线段 , 连接 . 点分别在线段上,连接与交于点 .
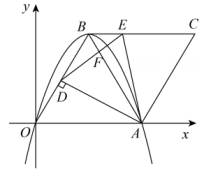 (1)、求点的坐标;(2)、随着点线段上运动.
(1)、求点的坐标;(2)、随着点线段上运动.①的大小是否发生变化?请说明理由;
②线段的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由;
(3)、当线段的中点在该二次函数的因象的对称轴上时,的面积为.17. 如图 (1)、【特例感知】如图23-1,对于抛物线 , 下列结论正确的序号是
(1)、【特例感知】如图23-1,对于抛物线 , 下列结论正确的序号是①抛物线都经过点;
②抛物线的对称轴由拋物线的对称轴依次向左平移个单位得到;
③抛物线与直线的交点中,相邻两点之间的距离相等.
(2)、
【形成概念】把满足(为正整数)的抛物线称为“系列平移抛物线”.
【知识应用】在(2)中,如图.①“系列平移抛物线”的顶点依次为 , 用含n的代数式表示顶点Pn的坐标,并写出该顶点纵坐标y与横坐标x之间的关系式;
②“系列平移拔物线”存在“系列整数点(横、纵坐标均为整数的点)”: , , 其横坐标分别为:为正整数),判断相邻两点之间的距离是否都相等,若相等,请求出相邻两点之间的距离;若不相等,说明理由.
③在②中,直线分别交“系列平移抛物线”于点 , 连接 , 判断直线是否平行?请直接写出判断结果.