2023-2024学年初中数学九年级上册 26.3 二次函数y = ax²+bx+c的图像 同步分层训练基础卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 二次函数y=x2-2x+3的图象的顶点坐标是( )A、(1,6) B、(1,2) C、(-1,6) D、(-1,2)2. 二次函数y=x2+bx+c的图象经过点(3,-8)和(5,-8),抛物线的对称轴是( )A、x=4 B、x=3 C、x=-5 D、x=-13. 抛物线的对称轴是( )A、直线 B、直线 C、直线 D、直线4. 如图,二次函数的对称轴为直线 , 下列判断正确的是( )
 A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 将二次函数配成顶点式后,发现其顶点的纵坐标比横坐标大1,如图,在矩形中,点 , 点 , 则二次函数与矩形有交点时的取值范围是( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 将二次函数配成顶点式后,发现其顶点的纵坐标比横坐标大1,如图,在矩形中,点 , 点 , 则二次函数与矩形有交点时的取值范围是( ) A、 B、 C、 D、6. 已知二次函数的解析式是y=x2-2x-3,结合图象回答:当-2<x<2时,函数值y的取值范围是( )
A、 B、 C、 D、6. 已知二次函数的解析式是y=x2-2x-3,结合图象回答:当-2<x<2时,函数值y的取值范围是( ) A、-4≤y<5 B、-4<y<5 C、-3≤y≤5 D、-4<y<-37. 二次函数的部分图像如图所示,其对称轴为直线 , 与x轴交于点A,点A的坐标为 , 则的值为( )
A、-4≤y<5 B、-4<y<5 C、-3≤y≤5 D、-4<y<-37. 二次函数的部分图像如图所示,其对称轴为直线 , 与x轴交于点A,点A的坐标为 , 则的值为( )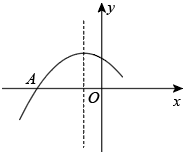 A、 B、0 C、1 D、28. 方程的根可视为函数的图象与函数的图象交点的横坐标,则方程的实根所在的范围是( )A、 B、 C、 D、
A、 B、0 C、1 D、28. 方程的根可视为函数的图象与函数的图象交点的横坐标,则方程的实根所在的范围是( )A、 B、 C、 D、二、填空题
-
9. 如图,在平面直角坐标中,抛物线和直线交于点和点 , 则不等式的解集为 .
 10. 抛物线y=x2+2x-1的对称轴是 .11. 二次函数图象的对称轴是.12. 如图,抛物线与y轴交于点A , 过的中点作轴,交抛物线于B、C两点(点B在C的左边),连接、 , 若将向上平移使得B、C两点恰好落在抛物线上,则点O平移后的坐标为 .
10. 抛物线y=x2+2x-1的对称轴是 .11. 二次函数图象的对称轴是.12. 如图,抛物线与y轴交于点A , 过的中点作轴,交抛物线于B、C两点(点B在C的左边),连接、 , 若将向上平移使得B、C两点恰好落在抛物线上,则点O平移后的坐标为 . 13. 若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:、都是“整点”,抛物线()与轴交于A、B两点,若该抛物线在A、B之间的部分与线段所围成的区域(包括边界)恰有6个整点,则m的取值范围是 .
13. 若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:、都是“整点”,抛物线()与轴交于A、B两点,若该抛物线在A、B之间的部分与线段所围成的区域(包括边界)恰有6个整点,则m的取值范围是 .三、计算题
-
14. 已知抛物线y=﹣2x2+(m﹣3)x﹣8.(1)、若抛物线的对称轴为y轴,求m的值;(2)、若抛物线的顶点在x正半轴上,求m的值.
四、解答题
-
15. 已知二次函数 . 若函数图象经过点(1,-4),(-1,0),求 , 的值.16. 已知二次函数的图象的顶点在x轴下方,求实数k的取值范围.
五、综合题
-