2023-2024学年初中数学九年级上册 26.2 特殊二次函数的图像同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-29 类型：同步测试

进入出卷网下载

一、选择题

1. 设函数 $y_{1} = - {(x - a_{1})}^{2}$ ， $y_{2} = - {(x - a_{2})}^{2}$ .直线 $x = 1$ 的图象与函数 $y_{1}$ ， $y_{2}$ 的图象分别交于点 $A (1 ， c_{1})$ ， $B (1 ， c_{2})$ ，得（）

A、若 $1 < a_{1} < a_{2}$ ，则 $c_{1} < c_{2}$ B、若 $a_{1} < 1 < a_{2}$ ，则 $c_{1} < c_{2}$ C、若 $a_{1} < a_{2} < 1$ ，则 $c_{1} < c_{2}$ D、若 $a_{1} < a_{2} < 1$ ，则 $c_{2} < c_{1}$

查看试题解析
2. 若点 $M (0 ， 5)$ ， $N (2 ， 5)$ 在抛物线 $y = 2 {(x - m)}^{2} + 3$ 上，则 $m$ 的值为（）

A、2 B、1 C、0 D、-1

查看试题解析
3. 抛物线 $y = 2 x^{2} - 4 x + 1$ 的对称轴是直线（）

A、 $x = - 3$ B、 $x = - \frac{3}{2}$ C、 $x = 1$ D、 $x = - 1$

查看试题解析
4. 抛物线 $y = 3 {(x - 1)}^{2} + 2$ 的顶点坐标为（）

A、 $(- 1 ， 2)$ B、 $(1 ， - 2)$ C、 $(1 ， 2)$ D、 $(2 ， 1)$

查看试题解析
5. 抛物线 $y = - 2 {(x - 3)}^{2} - 4$ 的顶点坐标（）

A、 $(- 3 ， 4)$ B、 $(- 3 ， - 4)$ C、 $(3 ， - 4)$ D、 $(3 ， 4)$

查看试题解析
6. 抛物线y＝ $\frac{1}{2}$ （x-3）²+1的顶点坐标为（）

A、（3，-1） B、（3，1） C、（-3、-1） D、（-3，1）

查看试题解析
7. 抛物线 $y = (x - 2)^{2} + 4$ 顶点的坐标是（）

A、 $(2 ， 4)$ B、 $(2 ， - 4)$ C、 $(- 2 ， 4)$ D、 $(- 2 ， - 4)$

查看试题解析
8. 已知函数 $y = {\begin{cases} {(x - 1)}^{2} - 1 (x \leq 3) \\ {(x - 5)}^{2} - 1 (x > 3) \end{cases}$ ，则使y=k成立的x值恰好有三个，则k的值为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

9. 二次函数 $y = {(x - 2)}^{2} + h (b \leq x \leq b + 1)$ 的图象上任意二点连线不与 $x$ 轴平行，则 $b$ 的取值范围为.

查看试题解析
10. 已知一个二次函数图象的形状与抛物线 $y = 2 x^{2}$ 相同，它的顶点坐标为 $(1 ， - 3)$ ，则该二次函数的表达式为.

查看试题解析
11. 已知二次函数 $y = 2 x^{2} + b x + 1$ ，当b取不同的值时，其图象构成一个“抛物线系”，如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象，它们的顶点在一条抛物线上（图中虚线型抛物线），则这条虚线型抛物线的解析式是 .

查看试题解析
12. 如图，在矩形 $A B C D$ 中，点N为边 $B C$ 上不与B、C重合的一个动点，过点N作 $M N ⊥ B C$ 交 $A D$ 于点M，交 $B D$ 于点E，以 $M N$ 为对称轴折叠矩形 $A B N M$ ，点A、B的对应点分别是G、F，连接 $E F$ 、 $D F$ ，若 $A B = 3$ ， $B C = 4$ ，当 $△ D E F$ 为直角三角形时， $C N$ 的长为．

查看试题解析
13. 如图，“心”形是由抛物线 $y = - x^{2} + 6$ 和它绕着原点O，顺时针旋转60°的图形经过取舍而成的，其中点C是顶点，点A，B是两条抛物线的两个交点，点E，F，G是抛物线与坐标轴的交点，则AB= ， FG= ， CE= ． ( 写出其中两个即可）

查看试题解析

三、解答题

14. 已知 $y$ 是关于 $x$ 的二次函数 $y = - \frac{1}{2} {(x - 2 m)}^{2} + 3 - m$ （ $m$ 是实数）．小明说该二次函数图象的顶点在直线 $y = - \frac{1}{2} x + 3$ 上，你认为他的说法对吗？为什么？

查看试题解析
15. 用配方法把二次函数 $y = - 2 x^{2} + 6 x + 4$ 化为 $y = a {(x + m)}^{2} + k$ 的形式，再指出该函数图象的开口方向、对称轴和顶点坐标.

查看试题解析

四、综合题

16. 如图，直线 $y = k x + 3$ 交x轴于A点，交y轴于B点，过A、B两点的抛物线的顶点坐标(1，4)．

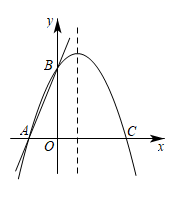
(1)、求k的值和抛物线的解析式；

(2)、在抛物线的对称轴上求一点P ，使得 $△$ PAB的周长最小，并求出最小值；

(3)、在抛物线的对称轴上是否存在点Q ，使 $△$ ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

查看试题解析
17. 如图，已知抛物线的方程y=－ $\frac{1}{m}$ (x+2)(x－m) (m>0)与x轴交于B、C，与y轴交于点E，且点B在点C的左侧，抛物线还经过点P(2，2)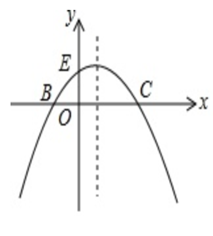

(1)、求该抛物线的解析式

(2)、在(1)的条件下，求△BCE的面积

(3)、在(1)的条件下，在抛物线的对称轴上找一点H，使EH+BH的值最小。求出点H的坐标。

查看试题解析

2023-2024学年初中数学九年级上册 26.2 特殊二次函数的图像 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 26.2 特殊二次函数的图像同步分层训练培优卷(沪教版五四制)