2023-2024学年初中数学九年级上册 25.4 解直角三角形的应用同步分层训练培优卷(沪教版五四制)

试卷更新日期：2023-07-29 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，为测量观光塔 $A B$ 的高度，冬冬在坡度 $i = 1$ ： $2.4$ 的斜坡 $C D$ 的 $D$ 点测得塔顶 $A$ 的仰角为 $53 °$ ，斜坡 $C D$ 长为 $26$ 米， $C$ 到塔底 $B$ 的水平距离为 $9$ 米 $.$ 图中点 $A$ ， $B$ ， $C$ ， $D$ 在同一平面内，则观光塔 $A B$ 的高度约为米 $. ($ 结果精确到 $0.1$ 米，参考数据： $s i n 53 ° \approx 0.8$ ， $c o s 53 ° \approx 0.6$ ， $t a n 53 ° \approx \frac{4}{3})$ （）

A、 $28$ 米 B、 $32$ 米 C、 $34$ 米 D、 $36$ 米

查看试题解析
2. “儿童放学归来早，忙趁东风放纸鸢”，小明周末在龙潭公园草坪上放风筝，已知风筝拉线长100米且拉线与地面夹角为 $65 °$ （如图所示，假设拉线是直的，小明身高忽略不计），则风筝离地面的高度可以表示为（）

A、 $100 s i n 65 °$ B、 $100 c o s 65 °$ C、 $100 t a n 65 °$ D、 $\frac{100}{s i n 65 °}$

查看试题解析
3. 河堤横断面如图所示， $B C = 5$ 米，迎水坡 $A B$ 的坡度是1：2（坡度是坡面的铅直高度 $B C$ 与水平宽度 $A C$ 之比），则 $A C$ 的长为（）

A、 $5 \sqrt{3}$ 米 B、 $10 \sqrt{3}$ 米 C、15米 D、10米

查看试题解析
4. 如图，一把梯子靠在垂直水平地面的墙上，梯子 $A B$ 的长是6米．若梯子与地面的夹角为 $α$ ，则梯子底端到墙面的距离 $A C$ 的长为（）米

A、 $6 \cdot c o s α$ B、 $6 \cdot s i n α$ C、 $\frac{6}{c o s α}$ D、 $\frac{6}{s i n α}$

查看试题解析
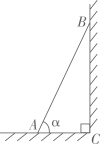5. 如图，大坝横截面的迎水坡AB的坡比为1：2，即BC：AC＝1：2，若坡面AB的水平宽度AC为12米，则斜坡AB的长为（）

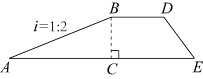A、4 $\sqrt{3}$ 米 B、6 $\sqrt{3}$ 米 C、6 $\sqrt{5}$ 米 D、24米

查看试题解析
6. 如图，某研究性学习小组为测量学校A与河对岸凉亭B之间的距离，在学校附近选一点C ，利用测量仪器测得 $∠ A = α$ ， $∠ C = 90 °$ ， $A C = 4 km$ ，则学校与凉亭之间的距离 $A B$ 等于（）

A、 $4 \sin α km$ B、 $\frac{4}{\sin α} km$ C、 $\frac{4}{\cos α} km$ D、 $4 \tan α km$

查看试题解析
7. 如图，为了量取垂直于地面的树高 $A B$ ，测量员站在距树6米的点C处，用倾角仪量得树顶端A的仰角为α ．若测倾角仪离地面高 $C D$ 为2米，则树高 $A B$ 的高可表示为（）

A、 $(2+6sinα)$ 米 B、 $(2 + \frac{6}{\sin α})$ 米 C、 $(2+6tanα)$ 米 D、 $(2 + \frac{6}{\tan α})$ 米

查看试题解析
8. 如图，在平面直角坐标系中， $A (6 ， 0)$ ， $B (0 ， 8)$ ，点C在x轴正半轴上，点D在y轴正半轴上，且 $C D = 6$ ，以 $C D$ 为直径的第一象限作半圆，交线段 $A B$ 于点E、F ，则线段 $E F$ 的最大值为（）

A、 $3.6$ B、 $4.8$ C、 $3 \sqrt{2}$ D、 $3 \sqrt{3}$

查看试题解析

二、填空题

9. 如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为45°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为120m，那么该建筑物的高度BC约为m（结果保留整数， $\sqrt{3} \approx 1.732$ ）．

查看试题解析
10. 如图，一航班沿北偏东 $60 °$ 方向从 $A$ 地飞往 $C$ 地，到达 $C$ 地上空时，由于天气情况不适合着陆，准备备降 $B$ 地，已知 $C$ 地在 $B$ 地的北偏西 $45 °$ 方向，则其改变航向时 $∠ α$ 的度数为．

查看试题解析
11. 如(图1)，某学校楼梯墙面上悬挂了四幅全等的正方形画框，画框下边缘与 $B$ 水平地面平行．如(图2)，画框的左上角顶点 $B$ ， $E$ ， $F$ ， $G$ 都在直线 $A B$ 上，且 $B E = E F = F G$ ，楼梯装饰线条所在直线 $C D / / A B$ ，延长画框的边 $B H$ ， $M N$ 得到平行四边形ABCD．若直线 $P Q$ 恰好经过点 $D$ ， $A B = 275 c m$ ， $C H = 100 c m$ ， $∠ A = 60 °$ ，则正方形画框的边长为

查看试题解析
12. 衢州儿童公园有摩天轮，水上乐园等娱乐设施，其中的摩天轮半径为20米，水上乐园的最高处到地面的距离为32米；如图，当摩天轮的座舱A旋转至与水上乐园最高处高度相同时，地面某观测点P与座舱A，摩天轮圆心O恰好在同一条直线上，此时测得 $∠ A P C = 30 °$ ，则 $P C$ 的距离为米；此时另一座舱B位于摩天轮最低点，摩天轮旋转一周要12分钟，若摩天轮继续逆时针旋转一周，当从座舱A观测座舱B的俯角为45°时，经过了分钟.

查看试题解析
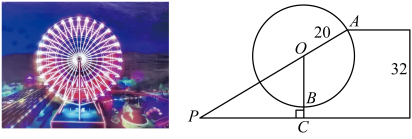13. 一款闭门器按如图1所示安装，支点A，C分别固定在门框和门板上，门宽 $O D = 52 c m$ ，摇臂 $A B = 18 c m$ ，连杆 $B C = 24 c m$ ，闭门器工作时，摇臂、连杆和 $O C$ 长度均固定不变.如图2，当门闭合时， $s i n ∠ B = \frac{\sqrt{5}}{3}$ ，则 $A C$ 的长为cm.如图3，门板绕点O旋转，当 $∠ B = 90 °$ 时，点D到门框的距离 $D K = 48 c m$ ，则 $O C$ 的长为cm.

查看试题解析

三、解答题

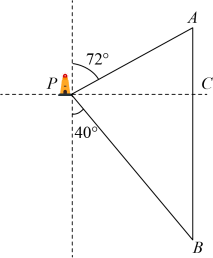
14. 如图，一艘海轮位于灯塔P的北偏东 $72 °$ 方向，距离灯塔 $100 n m i l e$ 的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东 $40 °$ 方向上的B处．这时，B处距离灯塔P有多远（结果取整数）？（参考数据： $s i n 72 ° \approx 0.95 ， c o s 72 ° \approx 0.31 ， t a n 72 ° \approx 3.08 ， s i n 40 ° \approx 0.64 ， c o s 40 ° \approx 0.77 ， t a n 40 ° \approx 0.84$ ．）

查看试题解析
15. 如图，某数学兴趣小组为了测量古树 $D E$ 的高度，采用了如下的方法：先从与古树底端 $D$ 在同一水平线上的点A出发，沿斜面坡度为 $i = 2 ： \sqrt{3}$ 的斜坡 $A B$ 前进 $20 \sqrt{7} m$ 到达点 $B$ ，再沿水平方向继续前进一段距离后到达点 $C$ ．在点 $C$ 处测得古树 $D E$ 的顶端 $E$ 的俯角为 $37 °$ ，底部 $D$ 的俯角为 $60 °$ ，求古树 $D E$ 的高度（参考数据： $s i n 37 ° \approx \frac{3}{5}$ ， $c o s 37 ° \approx \frac{4}{5}$ ， $t a n 37 ° \approx \frac{3}{4}$ ，计算结果用根号表示，不取近似值）．

查看试题解析

四、综合题

16. 随着科技的发展，无人机已广泛应用于生产生活，如代替人们在高空测量距离和高度．圆圆要测量教学楼 $A B$ 的高度，借助无人机设计了如下测量方案：如图，圆圆在离教学楼底部 $24 \sqrt{3}$ 米的C处，遥控无人机旋停在点C的正上方的点D处，测得教学楼 $A B$ 的顶部B处的俯角为 $30 °$ ， $C D$ 长为 $49.6$ 米．已知目高 $C E$ 为 $1.6$ 米．

(1)、求教学楼 $A B$ 的高度．

(2)、若无人机保持现有高度沿平行于 $C A$ 的方向，以 $4 \sqrt{3}$ 米/秒的速度继续向前匀速飞行，求经过多少秒时，无人机刚好离开圆圆的视线 $E B$ ．

查看试题解析
17. 小明家住在某小区一楼，购房时开发商赠送了一个露天活动场所，现小明在活动场所正对的墙上安装了一个遮阳棚 $B C$ ，经测量，安装遮阳棚的那面墙 $A B$ 高 $3 m$ ，安装的遮阳棚展开后可以使正午时刻房前能有 $2 m$ 宽的阴影处 $(A D)$ 以供纳凉．已知正午时刻太阳光与水平地面的夹角为 $63.4 °$ ，安装好的遮阳篷 $B C$ 与水平面的夹角为 $10 °$ ，如下右图为侧面示意图．

（参考数据： $s i n 10 ° \approx 0.17$ ， $c o s 10 ° \approx 0.98$ ， $t a n 10 ° \approx 0.18$ ， $s i n 63.4 ° \approx 0.89$ ， $c o s 63.4 ° \approx 0.45$ ， $t a n 63.4 ° \approx 2.00$ ）

(1)、据研究，当一个人从遮阳棚进出时，如果遮阳棚外端（即图中点C）到地面的距离小于 $2.3 m$ 时，则人进出时总会觉得没有安全感，就会不自觉的低下头或者用手护着头，请你通过计算，判断此遮阳棚是否使得人进出时具有安全感？

(2)、请计算此遮阳棚延展后的长度（即 $B C$ 的长度）．（结果精确到 $0.1 m$ ）

查看试题解析

2023-2024学年初中数学九年级上册 25.4 解直角三角形的应用 同步分层训练培优卷(沪教版五四制)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学九年级上册 25.4 解直角三角形的应用同步分层训练培优卷(沪教版五四制)