2023-2024学年初中数学九年级上册 25.4 解直角三角形的应用 同步分层训练基础卷(沪教版五四制)
试卷更新日期:2023-07-29 类型:同步测试
一、选择题
-
1. 爬坡时坡角与水平面夹角为α,则每爬1m耗能 , 若某人爬了1000m,该坡角为30°,则他耗能( ).(参考数据: , )
 A、58J B、159J C、1025J D、1732J2. 松华坝水库地处昆明北郊,是昆明市的重要水源,被称为“昆明头上的一碗水”,水库周边遍布森林与湿地,呈现出一幅纯净自然的和谐生态画卷.如图,大坝某段横截面迎水坡的坡度(),若坝高 , 则坡面的水平宽度长度约为( )(参考数据: , , )
A、58J B、159J C、1025J D、1732J2. 松华坝水库地处昆明北郊,是昆明市的重要水源,被称为“昆明头上的一碗水”,水库周边遍布森林与湿地,呈现出一幅纯净自然的和谐生态画卷.如图,大坝某段横截面迎水坡的坡度(),若坝高 , 则坡面的水平宽度长度约为( )(参考数据: , , )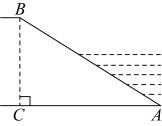 A、 B、 C、 D、3. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )
A、 B、 C、 D、3. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )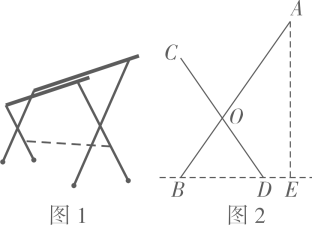 A、 B、 C、 D、4. 如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的 , 若山的高度米,则缆车索道的长为( )
A、 B、 C、 D、4. 如图,在天定山滑雪场滑雪,需从山脚下处乘缆车上山顶处,缆车索道与水平线所成的 , 若山的高度米,则缆车索道的长为( )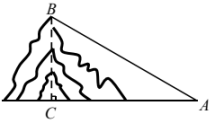 A、米 B、米 C、米 D、米5. 学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A、米 B、米 C、米 D、米5. 学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )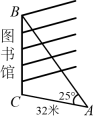 A、米 B、米 C、米 D、米6. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , )
A、米 B、米 C、米 D、米6. 日照灯塔是日照海滨港口城市的标志性建筑之一,主要为日照近海及进出日照港的船舶提供导航服务.数学小组的同学要测量灯塔的高度,如图所示,在点B处测得灯塔最高点A的仰角 , 再沿方向前进至C处测得最高点A的仰角 , , 则灯塔的高度大约是( )(结果精确到 , 参考数据: , ) A、 B、 C、 D、7. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( )
A、 B、 C、 D、7. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( ) A、米 B、米 C、米 D、米8. 如图,一航班沿北偏东方向从A地飞往C地,到达C地上空时,由于天气情况不适合着陆,准备备降B地,已知C地在B地的北偏西方向,则其改变航向时的度数为( )
A、米 B、米 C、米 D、米8. 如图,一航班沿北偏东方向从A地飞往C地,到达C地上空时,由于天气情况不适合着陆,准备备降B地,已知C地在B地的北偏西方向,则其改变航向时的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
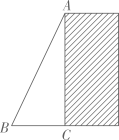
9. 如图,大坝横截面迎水坡AB的坡比为2:1,若坝高AC为12(m),则迎水坡AB的长为 (m).
 10. 如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=20m,则这棵树CD的高度约为 m.(按四舍五入法将结果保留小数点后一位,参考数据:)
10. 如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=20m,则这棵树CD的高度约为 m.(按四舍五入法将结果保留小数点后一位,参考数据:)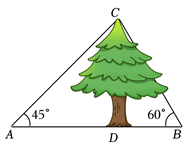 11. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号)
11. 综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为 , 尚美楼顶部F的俯角为 , 已知博雅楼高度为15米,则尚美楼高度为米.(结果保留根号) 12. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 .
12. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 . 13. 为发展城乡经济,建设美丽乡村,某乡对地和地之间的一处垃圾填埋场进行改造,把原来地去往地需要绕行到地的路线,改造成可以直线通行的公路 . 如图,经勘测,千米, , , 则改造后公路的长是千米(精确到千米;参考数据: , , , ).
13. 为发展城乡经济,建设美丽乡村,某乡对地和地之间的一处垃圾填埋场进行改造,把原来地去往地需要绕行到地的路线,改造成可以直线通行的公路 . 如图,经勘测,千米, , , 则改造后公路的长是千米(精确到千米;参考数据: , , , ).
三、解答题
-
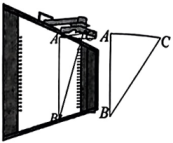
14. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC, . 黑板上投影图像的高度 , CB与AB的夹角 , 求AC的长.(结果精确到1cm.参考数据: , , )
 15. 今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且 , , 靠背 , 支架 , 扶手的一部分 . 这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据: , , )
15. 今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形是平行四边形,座板与地面平行,是等腰三角形且 , , 靠背 , 支架 , 扶手的一部分 . 这时她问小余同学,你能算出靠背顶端点距地面()的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据: , , )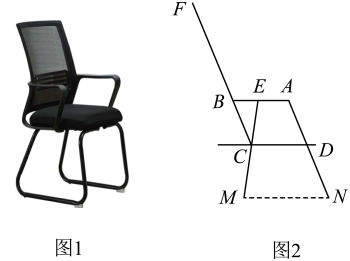
四、综合题
-
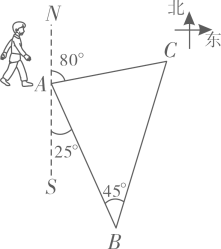
16. 为了增强学生体质、针炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点的南偏东方向处,点在点的北偏东方向,行进路线AB和BC所在直线的夹角为.
⑴求行进路线BC和CA所在直线的夹角的度数;
⑵求检查点和之间的距离(结果保留根号).
 17. 暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶高的山峰,由山底A处先步行到达处,再由处乘坐登山缆车到达山顶处.已知点A,B.D,E,F在同一平面内,山坡的坡角为 , 缆车行驶路线与水平面的夹角为(换乘登山缆车的时间忽略不计)
17. 暑假期间,小明与小亮相约到某旅游风景区登山,需要登顶高的山峰,由山底A处先步行到达处,再由处乘坐登山缆车到达山顶处.已知点A,B.D,E,F在同一平面内,山坡的坡角为 , 缆车行驶路线与水平面的夹角为(换乘登山缆车的时间忽略不计) (1)、求登山缆车上升的高度;(2)、若步行速度为 , 登山缆车的速度为 , 求从山底A处到达山顶处大约需要多少分钟(结果精确到)
(1)、求登山缆车上升的高度;(2)、若步行速度为 , 登山缆车的速度为 , 求从山底A处到达山顶处大约需要多少分钟(结果精确到)(参考数据:)